摘 要:为了分析地铁运营造成的环境低频(<20 Hz)振动,进行试验室低频振动试验研究。通过试验获得离散频率(5~16 Hz)简谐荷载下隧道内、地表和建筑物内的振动加速度信号,并对其进行预处理和归一化处理,从时程与频谱、加速度级和传递函数3个方面,分析低频振动在隧道结构、地表和建筑物内的传播特征。结果表明:隧道结构低频振动表现为整体振动,地表低频振动以竖向为主,而建筑物内的低频振动以水平方向为主;地表竖向低频振动随着距轨道水平距离的增加而衰减较快,水平低频振动在距轨道0~40 m范围内出现放大, 40 m之外衰减较缓;建筑物内的水平低频振动,在10 Hz以下随着楼层的升高而增大,而在10~16 Hz时随着楼层的升高而减小;隧道基底到地表的竖向传递函数值随着距轨道水平距离的增加而逐渐减小,但随频率变化不大,在5~16 Hz范围内的传递函数值为0~0.5。
关键词: 地下铁道; 低频振动; 环境振动; 试验研究; 传播特征; 加速度级; 传递函数
地铁以其运量大、速度快、安全可靠、运营准时等特点,已成为解决城市交通拥挤的一种有效措施。同时,地铁运营引起的环境振动问题引起了人们的普遍重视与研究。特别是近年来,地铁运营引发的低频(<20 Hz)振动对周围环境的影响备受国内外学者关注[1-6]。振动中的低频部分,由于其频率低,波长相对较长,穿越地层以及建筑物的能力强,将影响到一定范围内的地表环境和建筑物,甚至会影响到建筑物内的精密仪器和高技术设备的正常运行。
目前,国内对于低频振动的传播特征的研究成果很少[7-10]。为了更加深入地了解低频振动的传播特征,在北京交通大学轨道减振与振动控制试验室开展低频振动试验[11],分析和研究竖向和水平低频振动在隧道结构、地表和邻近建筑物内的传播特征,期盼为低频振动减振措施提供参考。
1 试 验
1.1 试验室概况
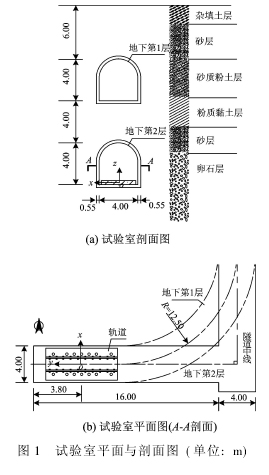
北京交通大学轨道减振与振动控制试验室是目前国内唯一建在地下的轨道与隧道工程试验室。试验室为上下双层结构,地下第2层为16.00 m长的直线隧道,地下第1层为12.50 m的小半径曲线隧道,地下第1层位于地下第2层上方4.00 m。上下2层隧道底板埋深分别为10.00和18.00 m ,隧道净宽和净高均是4.00 m,隧道壁厚0.55 m。试验室如图1所示。
1.2 轨道模型设计
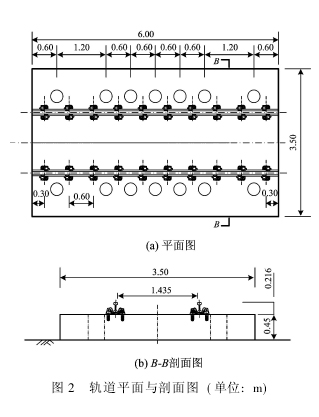
轨道模型布置在试验室的地下第2层(见图1),轨道纵向(Y方向)中间断面距隧道端部的距离为3.80 m。轨道模型结构如图2所示,设计比例为1∶1,采用C40混凝土现场浇注,轨道模型长6.00 m,截面宽和高分别为3.50和0.45 m。道床板上预留孔洞,用来安装钢弹簧,本次试验时不安装钢弹簧。钢轨选用T60轨;扣件采用DTVI2型扣件,其间距为0.60 m。
1.3 激振设备
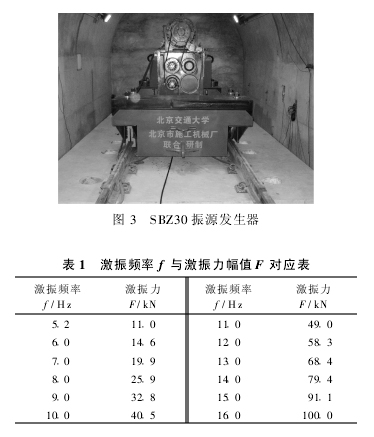
为了模拟列车对轨道结构的冲击载荷,课题组和北京施工机械厂合作研发了1台轨道振动源发生器SBZ30,如图3所示。SBZ30振源发生器能够模拟列车在铁轨上运行时对路基、桥基产生的动力状态,具有变频、变矩、变向的功能。SBZ30振源发生器主要工作频率在20 Hz以下,采用手动变矩,可产生竖向和水平方向激振力。SBZ30振源发生器由激振源和转向架构成,总质量为18 400 kg。激振源可以激发幅值变化范围0~250 kN的简谐荷载。转向架上有2个轮对,间距为2.2 m,与北京地铁列车的轴距接近。按照表1中的激振频率f改变激振设备的激振力幅值F,进行单频率试验。
1.4 数据采集设备
在试验中,采用2套数据采集设备分别用于隧道内、地表和建筑物内的振动测试。
在隧道内,采用高速便携式Wavebook/516E数据采集器和Lance AS105压电加速度传感器。数据采集器为以太网1 MHz采集器,包含Daq-view软件。Lance AS105压电加速度传感器的灵敏度约为251.5 mV·g-1,量程为20g,频率范围为0.35~6 000.00 Hz,分辨率为0.4×10-3g。
在地表和建筑物内,采用FOCUS Ⅱ动态信号采集分析仪和Lance AS系列高灵敏度加速度传感器。FOCUSⅡ动态信号采集分析仪是1套具有24位动态信号采集记录的系统,可以进行8通道同步输入,分析截止频率为42 kHz。Lance AS130传感器的灵敏度约为40 V·g-1,量程为0.125g,频率范围0.2~600.0 Hz,分辨率为0.5×10-6g。
1.5 测点布置
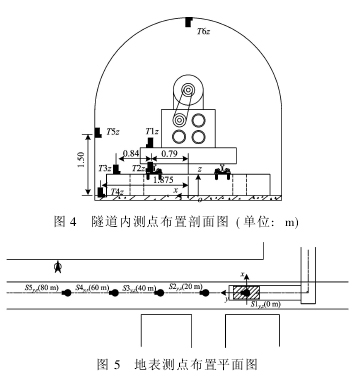
根据试验的需要,隧道内测点布置在轨道模型纵向中间断面(Y=0)上,选取6个测点T1,T2, T3, T4, T5和T6,分别位于激振器转向架、钢轨、道床板、基底、隧道侧壁和拱顶上,如图4所示。隧道内测点仅布置竖向加速度传感器。
地表测点布置选取轨道纵向中间断面(Y=0)的正上方地表点作为0 m处测点S1,沿着隧道中线依次选取20, 40, 60和80 m共4个测点S2,S3, S4和S5,如图5所示,布置了竖向和水平加速度传感器。
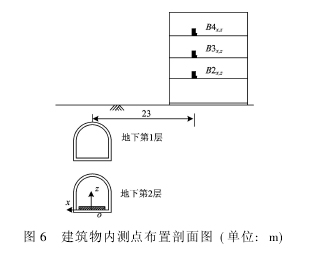
建筑物内共设置3个测点B2, B3和B4,距离隧道中线的水平距离均为23 m,如图6所示。在建筑物内,也布置了竖向和水平加速度传感器。
2 试验数据分析
在对试验测得的振动加速度信号进行分析之前,首先需对信号进行预处理[12,13],即消除趋势项和噪声部分,提取有用的信号。
在试验中,激振力大小随激振频率的变化而变化,其幅值可从11 kN变化到100 kN。为了便于比较同一激振力(单位激振力)下各个测点的响应水平,作如下假定。①测试对象体系处于小变形、小应变的弹性状态;②振动响应量值与激振力之间具有线性关系。为此,对测得的加速度信号进行归一化处理,选择单位激振力1 kN作为归一化标准。
对测试的加速度时程信号,经过预处理和归一化后,从时程与频谱、加速度级和传递函数等方面进行分析。
2.1 时程与频谱
限于篇幅,文中仅选取道床板(T3)、地表20m (S2)与建筑物4层(B4)共3处在激振频率f=8 Hz时典型的竖向加速度时程与频谱图进行分析,如图7所示。
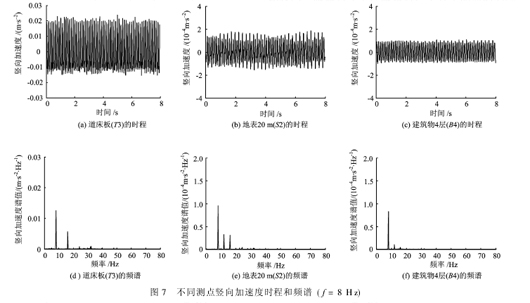
对不同测点、不同频率振动时程和频谱进行比较分析可以看出:在单一激振频率下,各个测点的加速度时程呈现周期性变化,整个体系呈稳态谐振响应;在单一的激振频率下,各个测点的响应频率与激振频率接近;道床板上的加速度量值远大于地表与建筑物内量值,且后两者接近。
2.2 加速度级
用信号的有效值衡量振动量的大小是一种比较好的方法,因为它涉及了振动时间变化的历经过程,与振动信号能量的含量有直接关系。对于离散信号的有效值(RMS),定义为
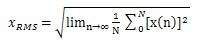
(1)
式中:x(n)是离散的各态历经的平稳信号序列;N是采样数据量。
为方便起见,采用加速度级代替加速度有效值。加速度级按下式定义[14]:
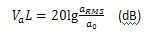
(2)
式中:
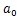
为参考振动加速度,
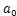
=10
-6m·s
-2;
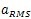
为某个位置的振动加速度有效值。
图8给出了隧道内各个测点的竖向加速度级。由图8可以看出:不同位置的加速度级变化趋势基本相同;转向架、钢轨和道床板上的振动量接近且大于其他测点;侧壁、基底和拱顶的振动量值也相互接近,可以认为隧道结构在低频激励作用下的振动表现为整体振动;由于激振设备的共振,在11~12 Hz范围内出现振动放大现象。
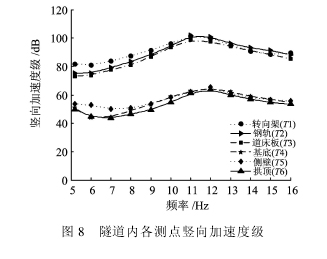
图9给出了地表各测点的竖向和水平加速度级。由图9可以看出:竖向加速度级大于水平加速度级;地表测点竖向和水平加速度级出现最大峰值的情形同隧道内测点竖向加速度级出现最大峰值的情形基本一致,在11~12 Hz范围内出现最大峰值;随着激振频率的增加,不同位置的竖向加速度级变化趋势基本相同;随着距轨道水平距离的增大,竖向加速度级减小, 20 m处的水平加速度级最大。
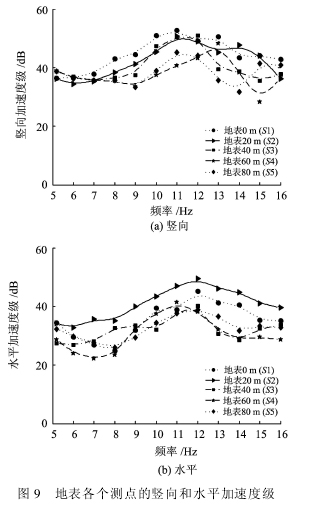
图10给出了建筑物内各个测点的竖向和水平加速度级。由图10可以看出:竖向加速度级小于或接近水平加速度级;建筑物内测点竖向和水平加速度级出现最大峰值的情形同隧道内和地表测点出现最大峰值的情形基本一致;随着激振频率的增大,不同位置的竖向加速度级的变化趋势基本相同;楼内测点的竖向加速度级量值很接近;在9Hz以下,随着楼层的增高,水平加速度级增大;在9~15 Hz范围内,随着楼层的增高,水平加速度级减小。
图11给出了不同频率下的竖向和水平加速度级随距轨道水平距离增大而衰减的情况。为了更好地表示这种衰减,引入加速度级梯度,其定义为加速度级差与水平距离差之比,即
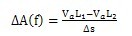
(3)
式中:f为频率;
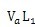
和
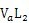
为不同距离处的加速度级;
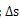
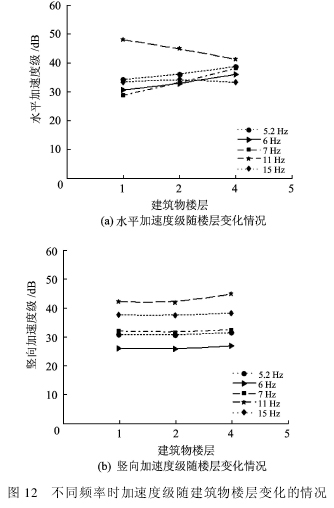
为水平距离差。
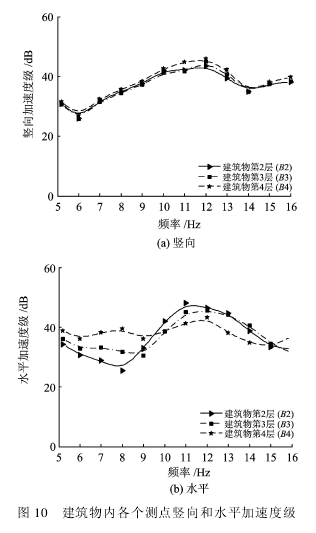

频率在16 Hz以下时,水平加速度级梯度有正有负,在20 m处出现明显的振动放大现象,而在40 m外,梯度变化不大。
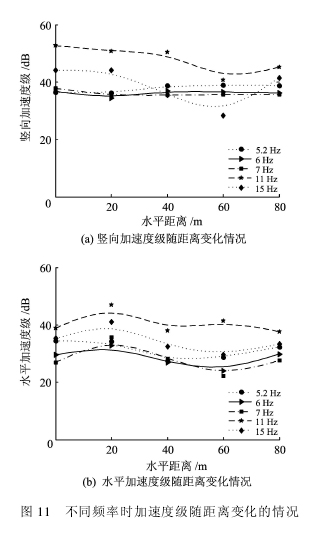
图12给出了不同频率下竖向和水平加速度级随建筑物楼层变化的情况。对于竖向加速度级,在各个频率下,随着楼层的升高而变化很小,各楼层加速度级接近。对于水平加速度级,频率在10 Hz以下时,随着楼层的升高而增大;在10~16 Hz范围内,随着楼层的升高而减小。
2.3 传递函数
振动的传递规律与轨道的形式、几何尺寸、材料及岩土特性、结构振动的基频等许多因素有关,是结构的固有特性;传递函数是结构固有特性的1种模型描述方式
[15]。传递函数建立在系统频域描述基础上,直接由系统的输入—输出关系获得其数学描述形式。设
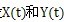
分别为系统的输入和输出,
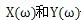
分别为系统的输入和输出的傅立叶变换,
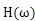
为系统的频率特性,即系统的传递函数,则有
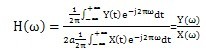
(4)
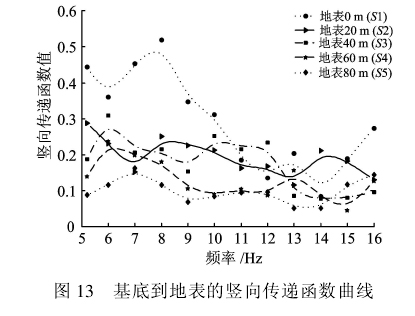
图13给出了基底测点与地表测点之间的竖向传递函数。可以看出:随着距轨道水平距离的增大,传递函数值减小;随着频率的增大,传递函数值变化不大,在5~16 Hz范围内的传递函数值在0~0.5之间。
3 结 论
(1)在试验条件下,隧道结构在低频激励作用下的低频振动表现为整体振动,地表低频振动以竖向为主,而建筑物内的低频振动以水平方向为主。
(2)地表竖向低频振动随着距轨道水平距离的增大而呈衰减趋势,即衰减梯度为正值;地表水平低频振动,在距轨道水平距离0~40 m范围内出现放大, 40 m之外呈微弱衰减趋势。
(3)建筑物内的低频竖向振动,随着楼层的升高而变化很小;而水平振动在10 Hz以下频率时,随着楼层的升高而增大,在10~16 Hz范围内,随着楼层的升高而减小。
(4)在单频激振条件下,随着距轨道水平距离的增大,隧道基底到地表的竖向传递函数值减小;随着频率的增大,传递函数值变化不大,在5~16Hz范围内的传递函数值在0~0.5之间。
参考文献
[ 1 ] WOLF S. Potential Low Frequency Ground Vibration (<6.3 Hz) Impacts from Underground LRT Operations [J].
Journal of Sound and Vibration, 2003, 267 (3): 651-661.
[ 2 ] 刘维宁,丁德云,孙晓静,等.北京地铁4号线北大段特殊减振措施研究[R].北京:北京交通大学, 2005.
(LIU Weining, DING Deyun, SUN Xiaojing, et al. Study on Special Vibration Reduction Measures in Beijing MetroLine 4 [R]. Beijing: Beijing Jiaotong University, 2005. in Chinese)
[ 3 ] SUN X J, LIU W N, ZHAI H, et al. Study on Vibration Effects upon Precise Instruments Due to Metro Train andMitigation Measures [ C ] //Environmental Vibrations: Prediction, Monitoring, Mitigation and Evaluation(ISEV2005). London: Taylor & Francis Group, 2005: 439-444.
[ 4 ] LIU W F, GUPTA S, DEGRANDE G, et al. Numerical Modelling of Vibrations Induced by Underground RailwayTraffic on Metro Line 4 in Beijing [R]. Leuven: K. U. Leuven and Beijing Jiaotong University, 2006.
[ 5 ] GUPTA S, LIU W F, DEGRANDE G, et al. Prediction of Vibrations Induced by Underground Railway Traffic inBeijing [J]. Journal of Sound and Vibration, 2008, 310 (3): 608-630.
[ 6 ] DING D Y, GUPTA S, LOMBAERT G, et al. The Prediction of Vibrations Induced by Underground Railway Traf-fic on Line 8 of Beijing Metro [R]. Leuven: K. U. Leuven and Beijing Jiaotong University, 2008.
[ 7 ] KRYLOV V V. Low-Frequency Ground Vibrations from Underground Trains [J]. Journal of Low Frequency Noiseand Vibration, 1995, 14 (1): 55-60.
[ 8 ] 丁德云,刘维宁,翟辉.地铁列车振动引发的地表低频(<10 Hz)响应的研究[C] //可持续发展的中国交通———2005全国博士生学术论坛(交通运输工程学科).北京:中国铁道出版社, 2005: 1106-1113.
(DING Deyun, LIU Weining, ZHAI Hui. Study on Ground Low-Frequency Response from Metro Train Induced Vi-brations [C] //China Sustainable Developing Transportation, 2005 National Doctoral Academic Forum (Transporta-
tion Engineering). Beijing: China Railway Publishing House, 2005: 1106-1113. in Chinese)
[ 9 ] 孙晓静.地铁列车振动对环境影响的预测研究及减振措施分析[D].北京:北京交通大学, 2008.
(SUN Xiaojing. Prediction of Environment Vibrations Induced by Metro Trains and Mitigation Measures Analysis
[D]. Beijing: Beijing Jiaotong University, 2008. in Chinese)
[10] LI K F, LIU W N, DING D Y, et al. Numerical Analysis of Low-Frequency Ground Vibrations Induced by MetroOperations [C] //Environmental Vibrations: Prediction, Monitoring, Mitigation and Evaluation. Beijing: Science
Press, 2009: 382-387.
[11] 丁德云,刘维宁,孙晓静,等.北京地铁4号线北大段特殊减振措施研究———浮置板轨道、梯形轨道实验室振动试验报告[R].北京:北京交通大学, 2007.
(DING Deyun, LIU Weining, SUN Xiaojing, et al. Study on Special Vibration Reduction Measures in Beijing MetroLine 4-Report of Vibration Measurements on the Floating Slab Track and Ladder Track in an Underground Lab [R].Beijing: Beijing Jiaotong University, 2007. in Chinese)
[12] 王济,胡晓. MATLAB在振动信号处理中的应用[M].北京:中国水利水电出版社,知识产权出版社, 2006.
[13] 孙延奎.小波分析及其应用[M].北京:机械工业出版社, 2005.
[14] 孙家麒,郭建国,金志春.城市轨道交通振动和噪声控制简明手册[M].北京:中国科学技术出版社, 2002.
[15] 王澜,宣言,万家,等.浮置板式轨道结构隔振效果仿真研究[J].中国铁道科学, 2005, 26 (6): 48-52.
(WANG Lan, XUAN Yan, WAN Jia, et al. The Simulation Research on the Vibration Insulation Performance of theFloating Slab Track Structure [J]. China Railway Science, 2005, 26 (6):