地下水水位上升对地铁隧道结构的影响
摘 要:在分析北京地区地下水水位上升情况的基础上,采用FLAC数值模拟方法,以拱顶埋深6 m、直径10 m的地铁隧道为例,研究地下水水位逐步回升情况下,隧道结构在位移、变形、内力(弯矩和轴力)、塑性区等方面的变化趋势和分布规律。分析结果表明,在地下水水位明显回升的情况下,隧道发生整体上浮、结构整体破坏的可能性不大,但会使隧道结构的内力(弯矩和轴力)发生变化,并且产生变形,会对地铁结构产生一定的影响。这些变化甚至有可能引起结构的开裂、渗水以及由此带来的一系列问题。因此在进行地铁、地下结构的规划、设计和施工过程中应对地下水的变化给予重视。
关键词: 隧道结构; 地下水; 水位上升; 结构内力; 变形; 位移、
自“十五”以来,随着一系列地下水开源节流的措施得到有力的贯彻和执行,特别是正在施工的南水北调工程对北京市水资源格局将造成重大影响,并可能由此造成地下水位的明显回升,形成新的城市地下水环境形态。根据国内外很多案例的分析[1-3],当地下水位回升时,可能会导致地铁和地下室、地下车库、地下管线、下穿式路堑等地下结构开裂、渗水、上浮和结构腐蚀等。关于地下水位回升对地下结构的影响已经引起广泛关注,但由于缺乏地下水位变化对结构影响的系统分析,因此对各种工程措施的评价缺乏坚实的依据。
本文在对北京地区地下水位上升情况进行分析的基础上,以地铁隧道为例,采用FLAC数值模拟方法,研究在地下水水位逐步回升的情况下隧道结构在位移、变形、内力(弯矩和轴力)、塑性区等方面的变化趋势和分布规律,为各类地下空间结构物的设计、运营期风险分析提供重要依据。
1 北京市地下水位的回升
近50年来,在首都大规模的建设和发展中,北京地下水资源严重超采,地下水位普遍下降。但是。近年来北京市采取了一系列水资源开源节流的措施。通过扩大再生水利用、建设生态水环境和一批重点水务工程以及改革水务管理体制等措施,到“十一五”结束时,北京全市总用水量将由39亿m3下降到34.5亿m3 [4]。另外,南水北调中线工程第1期将于2014年建成,届时每年将向北京市供水12亿m3;待2030年工程第2期建成,对北京的供水还将进一步加大。
从上面的初步分析看出,开源与节流措施涉及的水量占据了当前北京城市用水量相当大的比例,因此对北京水资源的供求平衡关系和水环境将产生重大影响。根据文献[4],在南水北调中线工程引水进京10年后,北京地区地下水位将普遍回升,最大将达到16 m,与文献[5]和文献[6]的结论基本一致。
根据国内外资料,很多大中城市由于人为干预而使地下水位回升,例如伦敦在减小地下水开采量后,水位最大上升幅度达到50 m。由于水位的明显上升造成了地铁隧道或车站渗水以及地铁电梯井筒变位而不能运行等问题。
水位回升的情况在北京也多次发生。例如,1985年后由于北京市地下水开采量每年减小3~4亿m3,使得1988—1992年间出现了区域性地下水位回升; 1995—1997年北京官厅水库放水也曾造成区域性地下水位的明显回升。
2 水位回升引起隧道整体上浮风险分析
北京地铁隧道大部分埋深都在10~30 m。当含水层中水位上升时,地层应力将产生变化,同时发生位移以及水压力增大,这些变化将对既有地铁结构产生一定的影响。例如结构因内力增大而导致不均匀变形,进而引起地下水渗入和结构的侵蚀。
2.1分析模型和计算步骤
假定1个圆形盾构隧道直径D为10 m (随隧道用途的不同,城市隧道的直径可能更大,例如北京地下直径线隧道直径达到11.60 m),拱顶埋深6m (即隧道的上覆土层厚度小于1.0D),轴心埋深11 m,土体为均质粉土地层且土体容重为2.01kg·m-3,地下水初始水位在隧道底下2 m。模型尺寸为50 m×30 m, FLAC2D剖分的计算网格如图1所示。计算中所采用的土体参数见表1,采用摩尔-库仑屈服准则。

由于本次模拟目的是为了分析地下水位的持续上升对地铁隧道的影响,因此在模拟计算时,先进行地铁隧道的盾构施工开挖,并完成衬砌结构的支护后,再考虑地下水位的变化对地铁隧道结构的影响。模拟计算的步骤如下:
(1)形成自重应力场,考虑地下水的作用,确定初始地下水位在隧道底下2 m (-18 m)处;
(2)模拟隧道开挖过程;
(3)衬砌支护,完成隧道的施工;
(4)初始化位移,不考虑隧道施工产生的位移;
(5)地下水位上升至隧道底部(-16 m);
(6)地下水位上升至隧道中部(-11 m);
(7)地下水位上升至隧道拱顶(-6 m);
(8)地下水位上升至隧道拱顶以上2 m (-4m);
(9)地下水位上升至地表(0 m)。
2.2 数值模拟计算结果分析
1)隧道与围岩的位移
通过上述模拟计算,得到隧道(拱底、拱顶)和地面(隧道中心上方)在各水位情况(工况)下的竖向位移如图2所示,各水位变化阶段产生的位移差见表2。
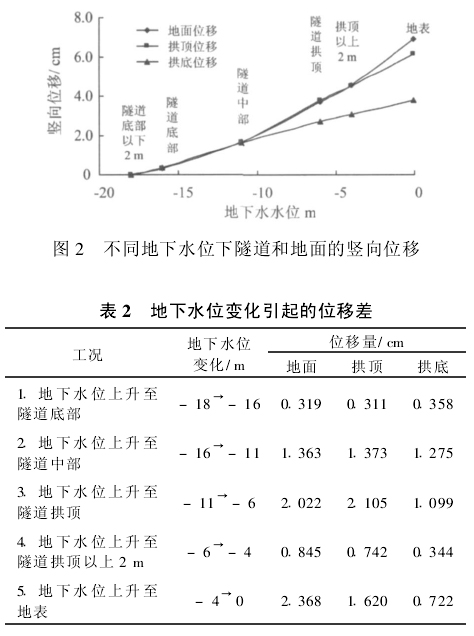
由图2和表2来看,总体上随着地下水位的持续上升,隧道和地层均不断产生向上位移,即由于地下水的浮力作用,使地面产生回弹变形和隧道发生上浮变形的趋势。该趋势随着水位的上升而不断明显,且有加快的趋势,具体分析如下。
工况1:当地下水位从隧道底下2 m (-18m)上升到隧道底部(-16 m)时,地下水并未对隧道产生浮力,但使隧道底部以下土中的孔隙水压力增加,土颗粒间的有效应力减小,引起土层的回弹,因此隧道和地层都发生了向上的位移。由于土层的回弹主要是由隧道下土体产生的,所以隧道产生整体的向上位移,而隧道本身的变形不明显,且拱底、拱顶和地表的位移量基本相同。
工况2:当地下水位从隧道底部(-16 m)上升到隧道中部(-11 m)时,除了上述土层的回弹外,地下水对隧道产生了浮力,但由于该浮力作用于隧道的下半部,因此并未引起隧道的变形,隧道仍然表现为整体上浮,且向上的位移较大。
工况3:当地下水位上升至隧道顶部(-6 m)时,浮力和水的侧向压力作用于整个隧道,隧道底部的孔隙水压力继续增加,隧道拱顶、拱底和地面也持续向上位移。其中隧道拱顶和地面的位移量约为拱底位移量的2倍,这是因为隧道拱顶及其以上土体受到的约束作用小(地面为自由面),因此容易产生变形;而隧道拱底受到土体的约束,不利于变形的发展。另外,通过对隧道中部水平位移的分析也表明:在地下水位上升至-11 m时,隧道中部的水平位移约为0.14 mm,随着地下水位继续上升至-6 m时,隧道中部的水平位移发生了很大的变化,为5.4 mm左右,这是因为隧道受到向内的挤压而变形的缘故。
工况4:当地下水位上升至隧道拱顶以上2m (-4 m)时,隧道和地层继续向上位移,但位移量大大小于工况3。在水位超过隧道后,作用在隧道上的浮力虽然不再增加,但随着地下水位的升高,作用于隧道结构上的侧向压力增加,隧道本身的变形继续增大,其中在隧道中部发生了7.4 mm的向隧道中心方向的水平位移,且地层的回弹变形也在继续增大。
工况5:当地下水位上升至地面(0 m)时,隧道和地层的变形趋势也非常明显,不再赘述。
2)隧道结构的变形
根据上述对地面及隧道拱顶和拱底位移的分析可知,在地下水位上升过程中,隧道结构主要产生2种变形,即侧向受压变形和竖向上移。
在初始状态下,隧道结构的变形主要是在拱底部分产生回弹,在拱顶部分产生沉降。以后随着地下水位的上升,隧道结构的拱顶、拱底和两侧均发生了一定的变形。在地下水位由底部上升到隧道中部的过程中,隧道结构本身基本未发生变形,但隧道由于土体的回弹而产生整体上浮,上浮量约为1.6 cm。
地下水位继续上升,则隧道拱顶、拱底向上的位移继续增大,而且由于侧向水压力的增大,隧道结构本身也产生了变形,在其两侧出现了向内的水平位移,这种水平位移在地下水位上升至地表时达到了1.22 cm。
3)土体中的塑性区
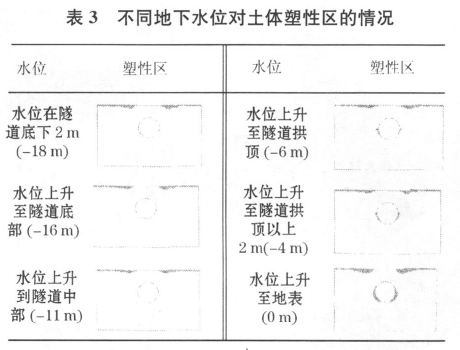
不同地下水位对土体中塑性区发展的影响见表3。由表3可以看到,在隧道正上方以外的地面附近产生了小范围的塑性区,而且该塑性区域在地下水位升至地表前基本没有继续发展,仅在地下水位上升至地表时才有小的扩展。这部分塑性区的产生可能是在隧道开挖过程中,由于上覆土较浅引起地层回弹变形,而使这部分土体承受了一定的拉应力造成的。
4) 隧道结构的内力情况
在地下水位逐渐上升过程中,隧道结构各典型位置(拱顶、拱底,结构的左右两侧)的弯矩发生了变化,如图3所示。
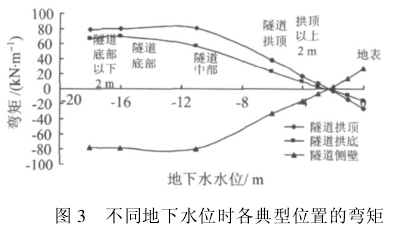
由图3可知,隧道结构各典型位置弯矩随地下水位的变化过程可分成3个阶段:地下水位低于隧道中部(-18~-11 m)为第1阶段;地下水位处于隧道中部以上、拱顶以下(-11~-6 m)为第2阶段;地下水位高于隧道拱顶(-6~0 m)为第3阶段。
在第1阶段,随着地下水位的升高,水平土压力减小,其在拱顶产生的负弯矩以及在拱底和结构两侧产生的正弯矩也减小,使得拱底处的正弯矩逐渐减小。对于拱顶处,由于其他荷载产生的弯矩不变,使得拱顶处的正弯矩增加。对于结构两侧,由于正弯矩减小,隧道结构两侧的最大负弯矩也略有增加(由-81.4 kN·m增大到-84.8 kN·m)。
在第2阶段,随着地下水位升至隧道拱顶部,水平土压力的弯矩变化与第1阶段类似,同时,竖向土压力在各处产生的弯矩也逐渐减小,再加上水压力产生的弯矩,使得各典型位置的弯矩均呈减小趋势。
在第3阶段,随着地下水位的上升,由竖向土压力和水平土压力在各典型位置产生的弯矩更小。在地下水位由地表下3 m升至地表下2 m的过程中,隧道各典型位置的弯矩虽然较小,但弯矩方向一直未发生变化;而随着地下水位的继续上升,由于竖向和水平土压力产生的弯矩更小,再加上水压力产生的弯矩,最终使隧道各典型位置的弯矩方向发生了改变,这对隧道结构的受力是非常不利的。
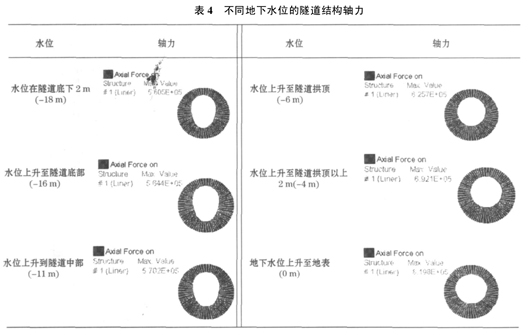
关于隧道结构轴力的变化,基本是随着地下水位的升高以及浮力和侧压力的增大也逐渐增大(见表4)。隧道结构轴力的最大值出现在地下水位到达隧道拱顶前的隧道结构两侧,之后,最大值出现在隧道拱底。隧道结构轴力的最大值从560 kN增大至820 kN,增幅达到46.4%,这将对隧道结构材料强度的安全性产生影响。
3 结 语
对于一般的城市地铁隧道,地下水位出现较大回升对隧道结构的内力和变形产生一定的影响,虽然隧道发生整体上浮、结构整体破坏的可能性不大,但很有可能产生结构的开裂,进而造成地下水的入渗,或受污染的地下水的侵蚀等。通过本文数值模拟计算的结果表明,地下水水位上升会对已建的地铁结构产生一定的影响,包括结构的弯矩和轴力都受到了影响,结构也发生了变形。因此,在地铁设计中应充分考虑地下水水位回升的影响。
由于本文分析考虑的是1种较为不利的情况(大直径隧道、浅覆土),且未考虑隧道的内重等荷载,简化了分析条件,而实际上隧道结构的受力状态更复杂,需要进一步充分考虑地层和隧道结构的特点,进行更深入、具体的分析。
参 考 文 献
[1] SIMPSON B, BLOWERT, CRAIG R N, et al. The Engineering Implications of Rising Groundwater Levels in theDeep Aquifer Beneath London [M]. London: CIRIA, 1989.
[2] HURST C W , WILKINSON W B. Rising Ground-Water Levels in Cities [J]. Proceedings of Conference onGroundwater in Engineering Geology, 1986 (3): 75-80.
[3] BRASSINGTON F C. Rising Groundwater Levels in the United Kingdom [J]. Proceedings of the Institution of Civ-il Engineers, 1990, 88: 1037-1057.
[4] 张在明,沈小克,王军辉,等.北京市地下水环境变化对结构抗浮影响研究[R].北京:北京市勘察设计研究院有限公司, 2009.
[5] 于秀治.南水北调后地下水位数值模拟预测及其环境影响评价[D].吉林:吉林大学, 2004.
(YU Xiuzhi. Groundwater Level Numerical Simulation Prediction and Its Environmental Influence Evaluation afterthe South-to-North Water Transferring Project [D]. Jilin: Jilin University, 2004. in Chinese)
[6] 孙颖,叶超,韩爱果,等.北京地区水资源养蓄方案初探[J].水土保持研究, 2006, 13 (6): 129-132.
(SUN Ying, YE Chao, HAN Aiguo, et al. The Protection and Accumulation Scheme of Water Resource of BeijingArea [J]. Research of Soil and Water Conservation, 2006, 13 (6): 129-132. in Chinese)