既有地铁车站结构安全性评估方法研究
摘 要:运用有限元程序及有限差分程序研究了新建地下风险工程对既有地铁车站结构的影响。结合既有车站双层风道与西南出入口结构之间的新建 3 号联络通道施工引起的位移分析,阐述了不同数值方法用于近接工程施工安全性评估的特点,并检算既有结构的承载力,结合既有结构现状调查结果,给出评估结论及推荐施工控制指标:地表沉降不超过 7 mm,地表隆起不超过 8 mm;车站底板隆起位移控制在 7 mm 以内,沉降缝两侧结构隆起位移差控制在 2 mm 以内;轨道的隆起位移不超过 5.8 mm,轨道水平不超过±0.6 mm。在上述位移控制指标范围内,得出新建隧道施工后既有地铁结构是安全的。
关 键 词:浅埋隧道;既有地铁车站结构;数值方法;安全性评估
1 引 言
近年来北京加快了城市地下轨道交通建设的步伐,预计 2012 年及 2015 年运营里程将分别达到420 km 和 561 km。完善的城市地下轨道交通网络将拥有众多的节点车站,必然存在新建地铁车站与既有运营车站之间换乘以及新建区间隧道穿越既有运营车站及线路的工程问题,如北京地铁 5 号线崇文门站和东单站、地铁 4 号线宣武门站和西单站、地铁 10 号线芍药居站和国贸站、机场线东直门站等。目前地铁及地下工程建设期的风险管理已经成为北京地下轨道交通建设管理的一个重要组成部分。风险管理按照工程进度可划分为 5 个阶段,即规划阶段、工可阶段、设计阶段、招投标阶段和施工阶段。对于设计阶段而言,被认定为重大风险源工程常进行既有结构的安全性评估,如正在规划设计的北京地铁 6 号线有车公庄、平安里、东四、朝阳门和呼家楼等车站在进行换乘及穿越既有地下结构时被认定为重大风险源工程,须对既有结构进行安全性评估。
国内有关新建地下结构近接施工对既有地下结构运营的安全性影响研究的相关文献还非常少。郑俊杰等[1]结合温福铁路琯头岭隧道下穿既有高速公路隧道工程,探讨了新建铁路隧道施工的主要技术方案及监控量测控制基准。王占生等[2]和张成平等[3-4]以北京地铁 5 号线崇文门暗挖车站下穿既有地铁隧道施工为背景,依据既有地下结构的检测评估和结构安全检算结果制定了既有地铁隧道结构和轨道的变形控制标准,并分析了施工监测数据,提出了相应的工程措施。张印涛等[5]利用三维有限差分程序研究了北京地铁某新建区间隧道采用矿山法近接施工下穿既有区间隧道的三维力学过程,并提出了施工优化方案。钱双彬等[6]对某隧道盾构施工近距离下穿既有地铁出入口人行通道进行了数值仿真分析,得出了地层变位规律及对结构内力和变形产生的影响,提出了运用水平位移、竖直位移、差异沉降、曲率和斜率等指标评价隧道盾构施工对近接既有结构的安全性影响。
总结已有的文献可知,新建隧道近接施工对既有地下结构的安全性影响的评估分析目前尚处于探索阶段,一些分析方法及评价指标还存在争议,如既有结构是采用旧规范还是新规范进行结构内力检算、分析模型是否考虑爆炸荷载等。本文结合拟建北京地铁 6 号线朝阳门及区间隧道的风险工程在设计阶段进行安全性评估,对既有车站结构及轨道的安全性评估方法进行有益探索。
2 既有结构及轨道安全性评估
2.1 安全性评估内容
既有结构安全性评估主要包含既有结构变形、强度检算和承载力检算。轨道安全性评估包括对轨道静态几何形位及线路调查按照容许偏差管理值[7]和对道床与结构的连接状况进行评估。新建风险工程近接施工对既有地铁结构的安全性影响评估的主要内容包括:①新建结构施工对既有地铁结构变形的影响;②对既有地铁结构、轨道及行车安全进行评估;③根据对结构及行车安全性影响评估结果,提出新建结构施工阶段沉降控制指标的建议值。
2.2 安全性评估方法
由空间计算模型分析得到新建地下结构施工过程中引起既有地铁结构及其附属结构的空间位移分布,着重分析既有地铁结构的空间不均匀位移、最大位移分布以及最大位移分布与施工计算步的关系,并结合结构中最大和最小主应力的分布,找出结构受力最不利的施工计算步、横断面、纵断面。新建地下结构施工扰动后,通过既有地铁结构受力最不利的横断面及纵断面的截面应力积分得到截面的内力,并且也可积分得出横断面和纵断面在施工扰动前的初始内力。既有地铁结构横断面和纵断面的设计承载力可通过结构原始设计图纸按相应的旧规范中有关计算公式计算得出。既有地铁结构安全评估步骤如图 1 所示。
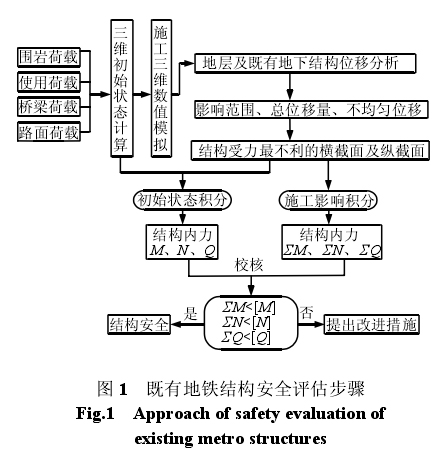
新建地下结构施工过程中,既有地下车站结构按正常使用工况考虑,同时应结合既有地下车站结构现状调查与检测结果,综合考虑和评价既有车站结构承载力的安全性。
轨道安全性评估方法:由于建模时考虑了线路轨道的位置,提取两股钢轨中心线上各节点的水平位移和竖向位移,并分析轨道的几何形位的变化,包括轨距、水平、轨向和高低。
3 工程实例
3.1 工程概况
拟建朝阳门站是北京地铁 6 号线的一个重要换乘站,与南北走向的既有 2 号线朝阳门站形成 T 型岛换乘。在车站及区间隧道工点初步设计过程中将2 号联络通道和 3 号联络通道工程列为二级风险工程,本文重点研究 3 号联络通道工程。
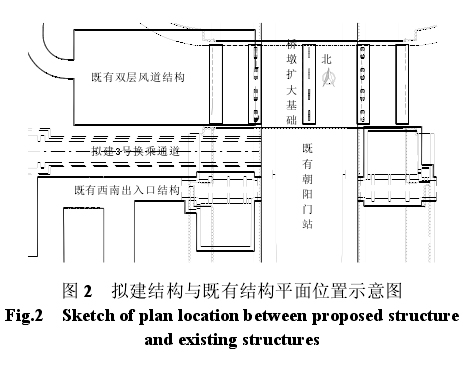
拟建 3 号换乘通道连接拟建朝阳门站 2 号换乘厅和既有 2 号线朝阳门站西侧侧墙,拟建 3 号换乘通道与既有朝阳门站、双层风道结构以及西南出入口结构之间的平面关系见图 2。双层风道结构与西南出入口结构之间的土体厚度为 11.1~12.3 m,而拟建 3 号联络通道位于既有双层风道和西南出入口结构之间,由扩大段和标准段组成,其中标准段长为 50.8 m,断面宽为 7.1 m,高为 6.25 m;联络通道与西南出入口结构之间的最小净距为 1.3 m,与风道结构之间的最小净距为 2.7 m;在既有车站西侧侧墙上开洞尺寸为 5.0 m×2.3 m。
既有 2 号线朝阳门站、车站双层风道及相关出入口修建于 20 世纪 70 年代,车站呈南北走向,全长为 141.18 m,宽为 22.7 m,为 3 跨框架结构,设有 4 道沉降缝,将车站分成 5 区段。轨道采用整体道床,道床为外露混凝土结构。既有双层风道的主体结构为整体框架结构,长为 44.1 m,宽为 22.7 m,并与既有车站之间设有 1 道沉降缝。既有西南出入口结构设有 2 道沉降缝,将通道分为扩大段、过渡段和出入口段,而扩大段与既有车站之间设有 1 道沉降缝。
3.2 数值模型简介
评估范围包括:既有车站南端,车站西侧以既有双层风道主体结构为限,并包括西南出入口结构的扩大段、过渡段和部分出入口段,既有车站东侧取 23.4 m,但不包括该范围内的东南出入口结构。
在安全评估范围内,除了局部边界范围内出现粉土③、粉细砂③3、中粗砂④4、圆砾卵石⑤外,地层主要为卵石填土①2、粉质黏土⑥夹粉土⑥2、圆砾卵石⑦等,因此,模型计算主要考虑了这 3 层土体。拟建 3 号联络通道完全位于卵石填土层中,数值模型如图 3 所示,共有单元 325 753 个,节点357 706 个。
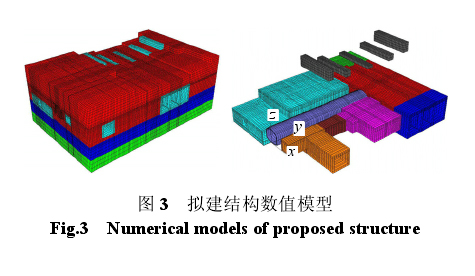
数值计算同时采用有限元 ANSYS 程序和有限差分 FLAC3D程序,在 ANSYS 程序中地层模型采用 D-P 破坏准则,而在 FLAC3D程序中地层模型采用摩尔-库仑破坏准则。模型中各地层的密度取天然密度,变形模量和泊松比取地勘报告的试验值或推荐值,但各地层的黏聚力和摩擦角取值的调整原则为 FLAC3D有限差分模型的初始应力场不出现塑性变形。地层及结构的力学参数如表 1 所示。
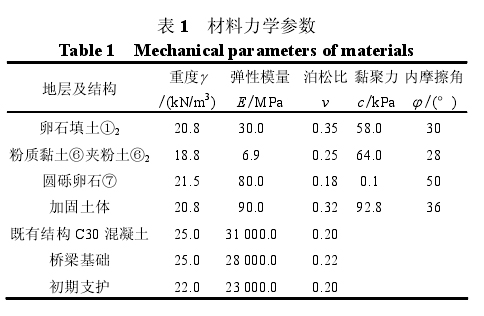
拟建 3 号联络通道施工模拟考虑了既有车站的两道沉降缝、双层风道与车站之间的沉降缝、西南出入口结构与车站之间的沉降缝、西南出入口结构的两道沉降缝共 6 道沉降缝。在 ANSYS 模型中,沉降缝采用弱化参数的实体单元模拟;而在FLAC3D模型中,沉降缝采用空气单元模拟,所谓空气单元即沉降缝两侧的实体结构单元不产生直接的相互作用,这样,由隧道开挖引起的既有结构段位移取决于既有结构段与周围地层的相互作用。
拟建联络通道施工方法为正台阶法。上台阶掌子面、拱部和边墙围岩超前注浆加固;模拟开挖最大进尺为 2.25 m,最小进尺为 1.00 m,平均进尺为1.66 m;上、下台阶土体分别分 27 步开挖完,下台阶土体开挖落后于上台阶 3 步,台阶长度为 3.50~6.31 m;边墙和拱部初期支护落后于上台阶开挖土体一步,仰拱初期支护落后于下台阶开挖土体两步。当隧道初期支护施工完后方可进行既有车站侧墙破洞施工。
路面车辆荷载取 20 kN/m2,车站站台人群荷载为 4 kN/m2,地铁车辆荷载为 33 kN/m2。桥梁路面以汽-20、挂-100 的车队荷载以及桥面自重荷载分别转化为桥台的均布荷载或桥基的集中荷载。
3.3 空间模型沉降分析
3.3.1 既有车站结构位移分析
不论是 ANSYS 模型还是 FLAC3D模型,既有车站结构第 2 段的整体位移都是最大的,其次是第1 段(北段),最后是第 3 段(南段),车站位移分析如表 2 所示。车站侧壁附近被开挖土体对车站侧壁有荷载和约束作用,随着联络通道的开挖及地层扰动,这种荷载和约束作用逐渐减小,直到最后消失,因此,既有车站整体上表现为隆起。
在车站底板建立 5 条考察纵向路径以分析车站底板的位移分布,如图 4 所示。由于 ANSYS 模型采用弱化参数的实体单元模拟沉降缝,因此,沉降缝两侧结构段并没有出现相对位移,如图 5 所示。但在 FLAC3D模型中沉降缝两侧的结构段出现了相对位移,最大相对位移为 3.58 mm,如图 6 所示。沉降缝的处理方式影响到车站结构的位移响应,在ANSYS 模型中第 1 段和第 3 段车站结构的位移将放大,而第 2 段结构的位移将缩小,而在 FLAC3D模型中第 1 段和第 3 段车站结构的位移将缩小,而第 2 段结构的位移将放大。
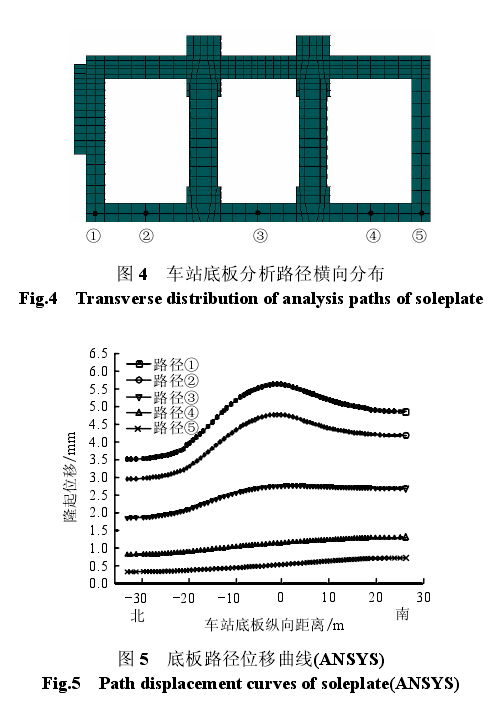
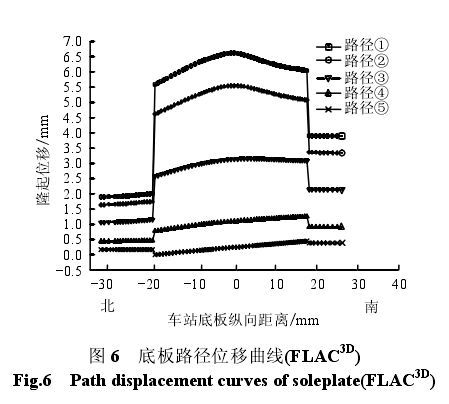
分析路径位移曲线可以得出:(1)对于路径④、⑤的隆起位移,ANSYS 的计算结果要大于 FLAC3D的计算结果;(2)对于路径①、②、③的隆起位移,在 ANSYS 模型中第 1 段和第 3 段结构的计算结果要大于 FLAC3D模型计算结果,而第 2 段结构的计算结果却小于 FLAC3D模型计算结果;(3)第 2 段结构产生了空间扭转变形。
分析路径①、③、⑤的位移分布曲线与施工步的关系可知,既有车站结构的位移随着施工掌子面与既有车站西侧侧墙之间的距离的减小而增大,而既有车站侧墙破洞引起车站自身的位移很小,ANSYS 模型为 0.29 mm,FLAC3D模型为 0.65 mm。
3.3.2 既有轨道位移分析
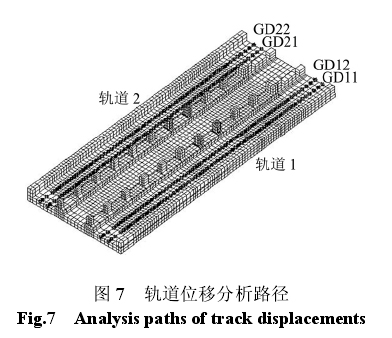
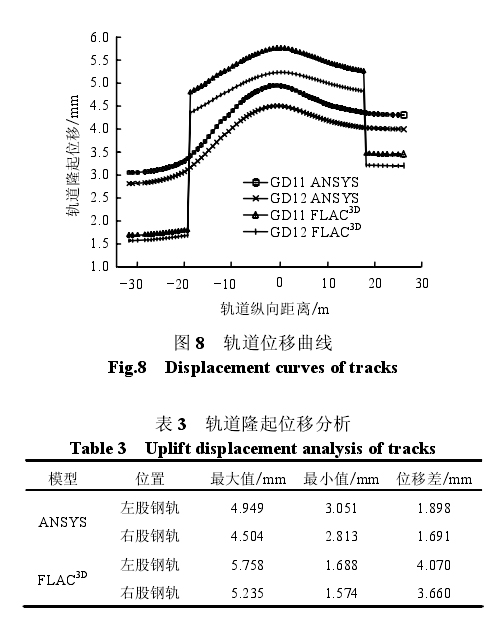
轨道 1(即 GD11 和 GD12,分别代表轨道 1 的左右股钢轨)和轨道 2(即 GD21 和 GD22,分别代表轨道 2 的左右股钢轨)分别位于车站西侧和东侧,如图 7 所示,轨道 1 受联络通道施工影响最大,因此,重点分析轨道 1 的静态几何形位的变形。
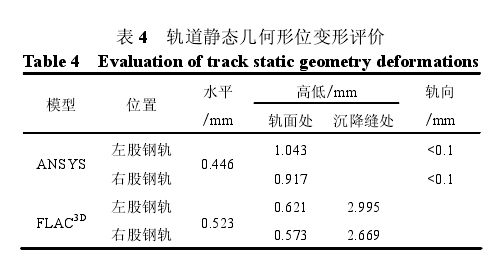
轨道 1 的左右股钢轨的隆起位移曲线如图 8 所示,在 FLAC3D模型中,隆起位移曲线存在隆起位移差,对于在沉降缝处没设接头的钢轨可解释为钢轨与整体道床之间存在变形差;对于在沉降缝处设有接头的钢轨可解释为钢轨隆起位移差。轨道隆起位移分析见表3,轨道静态几何形位变形评价见表4。
左右股钢轨出现整体性向新建联络通道侧的水平位移,在 ANSYS 模型中,水平位移最小值为1.010 mm,最大值为 1.239 mm,而轨距在±0.02 mm之间变化,因此,轨距变化可以忽略不计。
从表 4 可知,钢轨的轨向偏差远远低于计划维修容许偏差值 4 mm[7],左右股钢轨的水平偏差在计划维修容许偏差值 4 mm 范围内,轨道的高低偏差也在计划维修值 4 mm 范围之内。对于沉降缝处轨道,经过维修后不影响列车的正常安全运营。
3.3.3 不同数值模型位移分析的评价
对于位移模式,ANSYS 采用小应变大位移,而 FLAC3D采用大应变大位移;ANSYS 采用 D-P破坏准则,而 FLAC3D采用摩尔-库仑破坏准则,因此,两种数值分析方法采用不同的位移模式和破坏准则影响了地层的应力-应变响应,从而影响到地层及既有地下结构的最终位移。此外,沉降缝的模拟方法对地层及既有地下结构的最终位移也有较大影响。FLAC3D在模拟既有地下结构的沉降缝方面具有优势,对于拥有多道沉降缝的既有结构,采用FLAC3D模型是较好的选择。
就本文的数值模型而言,对于地层及既有地下结构的最大位移,FLAC3D模型的计算结果可能偏大,而 ANSYS 模型的计算结果可能偏小,但同时采用两种模型,可以对结构的变形进行相互印证。
3.4 既有结构承载力安全性评价
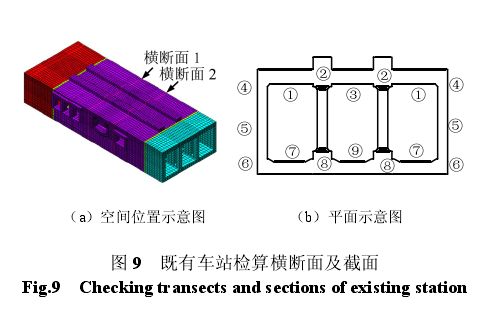
根据隧道施工后既有车站结构位移分布及变化特征、结构中大、小主应力分布,选定了 2 个检算横断面,横断面承载力检算位置如图 9 所示。①~⑨为检算截面编号。
对于既有结构承载力检算,横断面 1 和横断面2 的分析结论相同,隧道施工后既有车站结构横断面的各截面的弯矩、剪力都在设计范围内,以下以横断面 2 为例说明相关结果。隧道施工前后既有车站横断面 2 的弯矩分布如图 10 所示。各检算截面的设计抗弯、抗剪承载力、初始弯矩、剪力以及施工扰动后截面弯矩和剪力列于表 5。部分非重点考察截面的承载力计算值很小,表 5 中并未列出。
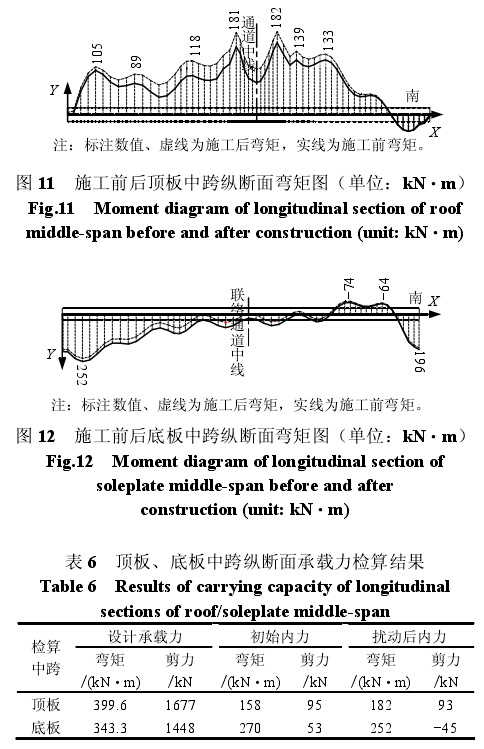
隧道施工前后既有车站顶板、底板中跨纵断面的弯矩分布分别如图 11、12 所示。顶板、底板中跨承载力检算结果列于表 6,分析结果表明,纵断面的抗剪承载力非常高,实际截面承受剪力非常小,截面弯矩也都在设计弯矩之内。
底板西梁的弯矩分布如图 13 所示。经计算,顶板、底板梁的设计承载力非常高,如底板西梁的截面弯矩的最小值为 10 603 kN·m,截面剪力为97 433 kN,而施工后梁承受的最大弯矩仅为设计弯矩的 17%,最大剪力仅为设计剪力的 19%。

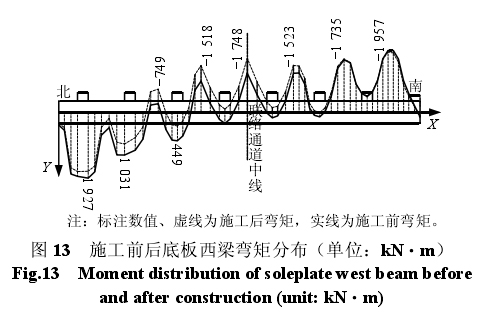
通过检算新建联络通道施工后既有车站结构横断面、纵断面以及顶梁、底梁的弯矩和剪力,对比分析其相对应的截面设计承载力,并结合既有结构现状调查报告[8],经综合评价认为,3 号联络通道施工及既有车站侧墙破洞完毕后既有车站结构是安全的。
4 典型既有地铁结构实测变形
通过总结近年来做北京既有地铁结构的安全性评估所累积的近接施工引起的既有地铁结构及轨道的实测变形,多个工程实例表明既有地铁结构的安全性评估时所推荐的既有结构及轨道的变形控制指标与实测变形偏差不大,这说明上述方法和经验适用于北京地区的类似工程。
首都机场线东直门站C区上跨并下穿既有地铁13 号线东直门站站后折返线,新建东直门站与既有折返线之间斜交。折返线隧道从地铁 13 号线东直门车站主体向南引出,在东直门外大街道路下为暗挖单层双联拱断面,13 号线车站主体和暗挖隧道之间为明挖单层单跨箱形结构。折返线明挖段长为14 m,宽为 12.3 m,高为 7.75 m,底板厚为 1 m,顶板厚为 0.85 m,侧墙厚为 0.9 m;折返线暗挖段宽为 12.05 m,高为 7.52 m,初支、二衬厚均为0.3 m,中墙厚为 0.5 m。新建隧道施工完成后既有结构及轨道的实测最终变形为:隧道结构最大沉降为-12.8 mm,变形缝最大差异沉降为 6.7 mm,变形缝开合度为 1.44 mm,轨道最大沉降为-12.8 mm,轨道水平变化为 1.4 mm,轨距变化为±1 mm。
南水北调总干渠暗涵采用暗挖法施工,并在左K5+102.694 和右 K5+115.361 处下穿北京地铁 1 号线五棵松车站,暗涵左右隧道中心线的距离为8.2 m,分别与地铁 1 号线里程 B87+26.3、B87+38.7交叉,毛洞开挖的顶部距五棵松车站底部仅为3.7 m。穿越部分暗涵隧道结构型式为两孔分离φ 4.0 mm 钢筋混凝土圆涵。地铁五棵松车站于 20世纪 60 年代建成,采用明挖法施工,为单层 3 跨的矩形框架结构。车站呈东西走向,车站主体全长为174.98 m,宽为 19.5 m,底板高程为 46.767 m。新建隧道施工完成后既有结构及轨道的实测最终变形:车站底板结构最大沉降-4.8 mm,道床结构最大沉降为-3.9 mm,变 形缝最大差异沉降为±2.5 mm,变形缝开合度为 0.9 mm,无缝钢轨最大位移为-0.5 mm,轨道水平变化为±1 mm,轨距变化为±1 mm。
郑常庄热电厂新建电力隧道下穿北京地铁 1 号线万寿路站。新建电力隧道为盾构法施工,隧道埋深为 23.8~24.5 m,盾构隧道外径为 3.64 m,内径为 3 m。万寿路站位于复兴路下方,东西向布置,全长为 146.78 m,有效站台处车站全宽为 17.7 m,车站中心里程为 B105+12,对应位置车站结构外顶标高为 51.333 m。新建电力隧道与既有地铁车站结构正交,对应地铁右线里程为 B105+07.231。电力隧道与既有车站底板的垂直距离为 13.0~13.7 m。新建隧道施工完成后既有结构及轨道的实测最终变形:隧道结构最大沉降及差异沉降为-0.8 mm,轨道最大沉降及差异沉降为±0.6 mm,无缝钢轨最大位移为 0.2 mm,轨道水平变化为±2 mm,轨距变化为±2 mm。
5 结 论
(1)FLAC3D在材料库及模拟地层大变形、软弱地层等方面具有优势,同时对既有结构沉降缝的处理较灵活,能够模拟出沉降缝的力学效应;相对而言,ANSYS 模拟软弱地层、既有结构沉降缝方面并无优势,甚至还很困难。
(2)就本文数值模型,对于地表沉降,FLAC3D模型的计算结果小于 ANSYS 模型的计算结果,但对于地表及既有车站结构的隆起位移,FLAC3D模型的计算结果大于 ANSYS 模型的计算结果。
(3)新建 3 号联络通道施工及既有车站侧墙破洞完毕后地面最大沉降为 ANSYS 模型得出的6.47 mm,最大隆起为 FLAC3D模型得出的 7.27 mm(本文以既有地下结构变形和承载力为论述重点,因而省略了地面位移(即沉降或隆起)分析部分);以下数值均来自 FLAC3D模型的计算结果,车站底板的最大隆起为 6.875 mm,沉降缝两侧结构位移差3.58 mm;轨道的最大隆起为 5.758 mm,最小隆起为 1.574 mm,沉降缝处轨道的隆起位移差最大值为2.995 mm,轨道水平变化为 0.523 mm。
(4)综合数值模拟结果、已积累的相关工程的实际最终量测值及地铁列车运营相关规程,给出在既有双层风道与西南出入口之间的新建 3 号联络通道施工建议控制指标:地表沉降不超过 7 mm,地表隆起不超过 8 mm;车站底板隆起位移控制在7 mm 以内,沉降缝两侧结构隆起位移差控制在2 mm 以内;轨道的隆起位移不超过 5.8 mm,轨道水平变化±0.6 mm。
(5)对于新建联络通道施工前后既有车站结构检算横断面及纵断面的应力状态,ANSYS 模型的计算结果大于 FLAC3D模型的计算结果,因此,结构承载力安全性评价主要是基于 ANSYS 的计算结果,分析检算结果表明,如果既有车站结构变形在建议控制指标范围内 3 号联络通道施工及既有车站侧墙破洞完成后既有车站结构是安全的,经过维修后不影响列车的正常安全运营。
参 考 文 献
[1] 郑俊杰, 包德勇, 龚彦峰. 铁路隧道下穿既有高速公路隧道施工控制技术研究[J]. 铁道 工程学报, 2006, (8):80-84.
ZHENG Jun-jie, BAO De-yong, GONG Yan-feng. Research on construction control technology for railway tunnel underneath passing existing expressway tunnel[J].Journal of Railway Engineering Society, 2006, (8): 80-84.
[2] 王占生, 张顶立. 浅埋暗挖隧道近距下穿既有地铁的关键技术[J]. 岩石力学与工程学报, 2007, 26(增刊 2):4208-4214.
WANG Zhan-sheng, ZHANG Ding-li. Key techniques on shallow embedded tunnel constructed beneath existing subway tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(Supp.2): 4208-4214.
[3] 张成平, 张顶立, 王梦恕. 复杂地铁工程施工安全控制技术研究[J]. 中国安全科学学报, 2008, 18(8): 171-176.
ZHANG Cheng-ping, ZHANG Ding-li, WANG Meng-shu. Research on safety control techniques for complex subway construction[J]. China Safety Science Journal,2008, 18(8): 171-176.
[4] 张成平, 张顶立, 吴介普, 等. 暗挖地铁车站下穿既有地铁隧道施工控制[J]. 中国铁道科学, 2009, 30(1): 69-73.
ZHANG Cheng-ping, ZHANG Ding-li, WU Jie-pu, et al. Construction control of a newly-built subway station undercrossing the existing subway tunnel[J]. China Railway Science, 2009, 30(1): 69-73.
[5] 张印涛, 陶连金, 张飞劲, 等. 矿山法开挖近距离下穿越既有线隧道的三维数值模拟[J]. 北京工业大学学报,2007, 33(12): 1273-1277.
ZHANG Yin-tao, TAO Lian-jin, ZHANG Fei-jin, et al. Numerical modeling of tunneling cross under ultra-near metro tunnel[J]. Journal of Beijing University of Technology, 2007, 33(12): 1273-1277.
[6] 钱双彬, 董军, 李玲. 隧道盾构施工下穿地铁车站出入口安全影响分析[J]. 中国安全科学学报, 2009, 19(1):172-176.
QIAN Shuang-bin, DONG Jun, LI Ling. Analysis of thesafety influence of shield tunnel construction on its abovemetro station[J]. China Safety Science Journal, 2009,19(1): 172-176.
[7] 王玮, 梁柏成, 吴建中, 等. 北京地铁工务维修规则(试行)[M]. 北京: 北京地铁运营有限责任公司, 2002.
[8] 郭盛, 赵智涛,丁振明, 等. 北京地铁 2 号线朝阳门站现状调查[R]. 北京: 北京市建设工程质量第三检测所, 2009.