摘  要：针对盾构掘进过程中引起的两相水平位移，对广州地铁 2、8 号延长线某区间进现场实测，将实测结果与数值模拟相结合，计算表明，在盾构通过的不同阶段，平行于隧道方向的水平位移 U₁与垂直于隧道方向的水平位移 U₂呈现出不同的变化规律，在 1 倍隧道直径的区域内，U₁位移最大值大于 U₂位移最大值，两相位移均不可忽略。

关键词：盾构施工；ABAQUS；三维有限元；动态模拟；水平位移；沉降

 

      盾构开挖引起土体竖直沉降导致沉陷槽在国内外已有广泛研究，随着 1969 年美国 Peck^[1]指出隧道掘进引起的地表沉降曲线满足正态分布，盾构法隧道施工变形的经典预测理论与方法初步形成。

      随着城市发展，压力注浆及地表沉降控制已经逐渐成熟。朱合华^[2]通过引入等效孔隙率来考虑建筑间隙的影响，对浆液渗透范围及管片的注浆压力进行了理论推导。丁春林等^[3]采用弹塑性有限元法得出随着地应力释放值增加，隧道开挖面洞周、拱顶、拱底、拱腰变形增大，地表沉降变形也大大增加。

      然而，地层的总体位移分为水平位移和竖向位移，水平位移又分为纵向和横向两相位移。当隧道穿越地下构筑物时，地层水平位移和竖向位移的叠加共同影响构筑物的总体位移，目前国内一些学者针对盾构开挖引起的水平位移有了一定研究，施成华等^[4]应用随机介质理论，对隧道施工所引起的纵向地层移动与变形进行了分析，推导了相应的计算公式。王占生、王梦恕^[5]等提出了一种预测盾构隧道施工引起地表下土体水平变位的简便估算方法，并结合 Mair 计算公式对盾构隧道施工引起的地表下土体沉降变位进行了预测。而对于在盾构开挖过程中，两相水平位移随时间的运动趋势以及两者之间的大小关系，还需进一步研究探讨。

      广州市轨道交通 2、8 号延长线洛溪－南洲区间详 细勘察范围 线路起止里 程为 YCK7+621 ～YCK9+854，隧道全长 2 233 m，均采用盾构法施工。在广州地铁 2、8 延长线隧道左线里程 ZDK8+164.437～ZDK8+182.437 范围处，分别在隧道开挖轴线上方、斜上方布设测点，以测得土层的位移扰动情况，总结出盾构开挖过程中土体水平位移的变化趋势，为今后预测广州地区盾构掘进对地下以及周边构筑物的影响提供依据。

 

      试验场地地貌属珠江三角洲冲积平原，微地貌单元属河流冲积阶地，地面平坦。本区间采用两台德国海瑞克公司生产φ 6 250 mm 复合式土压平衡盾构机，隧道轴线位于地表以下 29.3 m 处，隧道开挖所在层为岩石层。本试验经协调，最终选定于广东长大物业发展有限公司一废弃仓库中进行量测。取最近钻孔 MBZ3-LN-14 号钻孔的地质资料，通过Peck 沉陷槽理论公式（1）计算出隧道开挖沉陷槽宽度 B 来布置各测点位置。土体各层参数如表 1 所示。

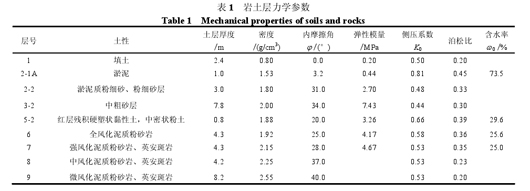
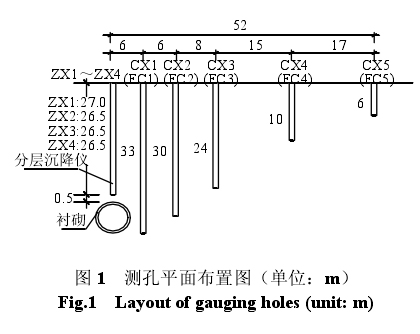
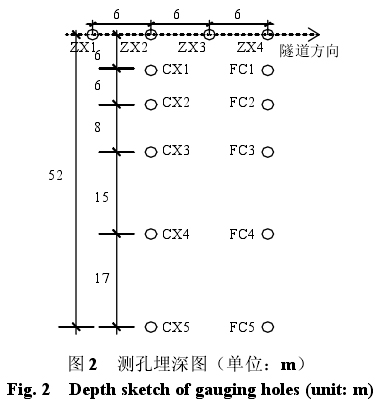
      由现场资料及钻孔柱状图，隧道埋深 D =29.3 m，根据地质报告，各层土取加权平均后的内摩擦角 φ=30.2°，由式（1）计算得出横向沉陷槽宽度系数 i，由此可得出沉陷槽宽度 B =50.862 m。现场距隧道轴线上方最远测点(CX5 和 FC5)距轴线52 m，大于估算的沉陷槽宽度 50.862 m，满足要求。其现场测孔平面布置图及埋深图如图 1、2 所示。

      本试验场地管口位置采用全站仪进行定位，以较远处的立交桥墩作为固定点，在盾构通过前测得初始值，之后在盾构开挖过程中依次测量，以确定地表管口的实际二维水平位移变化，由此来确定各地层的实际水平位移。地表竖向位移采用水准仪，仍用桥墩固定点进行测量。本试验测斜仪深入管底后，每提升 1 m 读一次数，正反两次取平均值以消除初始零偏；分层沉降仪每上提 3 m 遇到磁环后读一次数，磁环通过膨胀黏土球与周围土体紧密相连，以保证磁环与周围土层位移的同步性。当盾构刀盘位于ZX1测点15 m远时开始读数，当刀盘离开ZX4测点 30 m 后停止读数。读数过程中在盾构机通过测点时读数频率为 1～2 次/h，通过后适当放宽读数间隔，以测得其沉降变化全过程。

      Peck 地表沉降槽理论^[1]认为，地表以下至隧道以上各土层沉陷槽体积应等于地层损失的体积，而且沉降槽仍为正态分布曲线，随着土层深度 z 的增大，该土层距隧道顶部的垂直距离减小，土层的沉降槽曲线宽度系数将会减小，即式（1）中 S_max和 i两个参数的取值会随深度变化而不同，它们均可表示为深度 z 的函数：

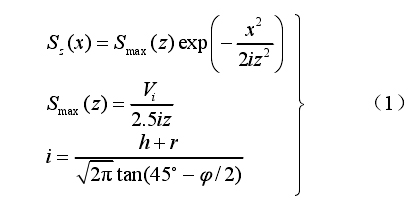
式中： S_s( x)为距隧道中心线横向距离x处的地表沉降；S_max为地表的最大沉降值；i为沉降槽宽度系数,取为地表沉降曲线反弯点与原点的距离；V_i为盾构隧道单位长度地层损失量； φ为土体的内摩擦角；h为覆盖层的厚度；r为盾构半径。

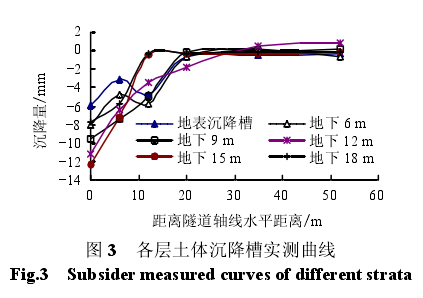
      图3为盾构刀盘通过分层测点约40.5 m后该时刻各层土体沉降槽曲线，此时认为隧道开挖造成的瞬时沉降已经完成。由图可知，对隧道上方各层土体，盾构施工引起的沉降量随土层深度而增加，沉降槽宽度随之减小。地表土体沉降槽宽度约为52 m，地下 6 m 处沉降槽宽度约为 35 m，地下 12 m沉降槽宽度约为 30 m，地下 18 m 沉降槽宽度约为12 m，实测土体位移规律与 Peck 沉降槽理论基本吻合。

      为考察不同地层之间的水平位移变化情况，图4～9 给出了以地面为基点的相对水平位移。由于篇幅所限，且 5 个测管水平位移趋势一致，因此，本文仅给出距隧道最近且变化显著的 CX1、CX2、CX3 3 个测管的位移曲线。

      图 4 为盾构在行进过程中，测斜管 CX1 在垂直于隧道开挖方向的水平位移变化图。由图可知，在盾头距离测点还有 4.5 m 处时，土体向隧道外侧排开，埋深 28 m 处水平位移达到最大值 8.4 mm；在通过测点 3 m 时回缩最大，埋深 28 m 处水平位移最大值仅为 3.04 mm；当盾头通过测点后，在压力注浆的作用下，土体被排开，在盾头通过测点 24 m时，土体被排开达到最大，埋深 27 m 处水平位移达到最大值 22.04 mm；之后盾构机停顿 2 d，土体出现轻微的回缩，在盾头通过测点 25.5 m 时，隧道周围土体仍旧向外被排开，埋深 29 m 处水平位移达到最大值 20.93 mm，但该值小于盾头通过测点18 m 时的水平位移 21.24 mm，可以认为，在盾构向前开挖过程中，在通过 CX1 测点 24 m 时达到最大位移，由图还可以看出，压力注浆的后期影响作用显著。

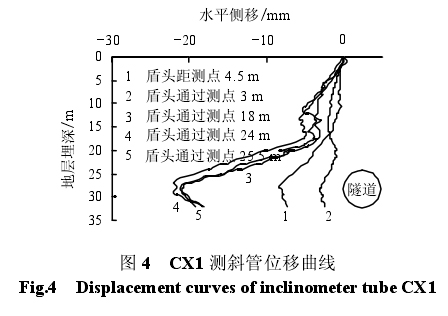
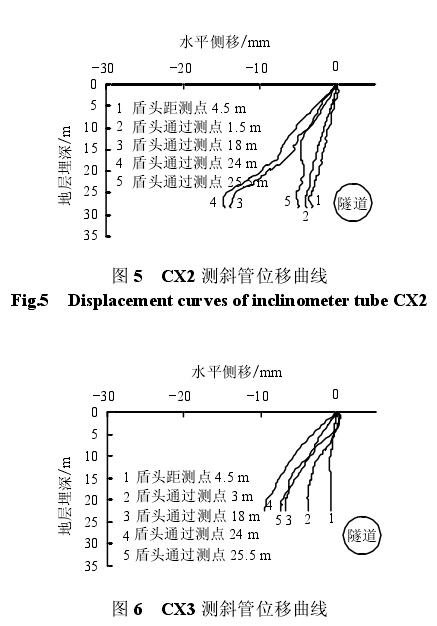
      图 5、6 为盾构在行进过程中，CX2、CX3 测斜管在垂直于隧道开挖方向的水平位移变化图，综合来看，距离隧道越远的测点，在隧道开挖影响下水平位移越小，且基本运行规律与 CX1 测点一致，当盾构通过测点 24 m 后，压力注浆发挥到最大值，之后由于洞口应力释放及浆液固化出现回缩现象。

      图 7 为盾构在行进过程中，CX1 测斜管在平行于隧道开挖方向的水平位移变化图。在盾构距离测点 4.5 m 处时，在隧道轴线方向的土体便开始向前方移动，埋深 29 m 处水平位移达到最大值22.23 mm；此后盾构机继续向前方移动，当盾头通过测点 3 m 时（此时盾构机身仍旧处于通过当中），土体沿隧道开挖方向位移在埋深 29 m 处达到最大值35.20 mm；当盾构完全通过后，由于盾构千斤顶作用点在衬砌上，使得衬砌与周围土体围岩发生负横向摩擦，导致土体 U₁方向位移转而向着隧道开挖负方向运动，当通过测点 25.5 m 时回缩到最小，说明在盾构离开测点 25.5 m 后，土体仍然有向后的水平位移。

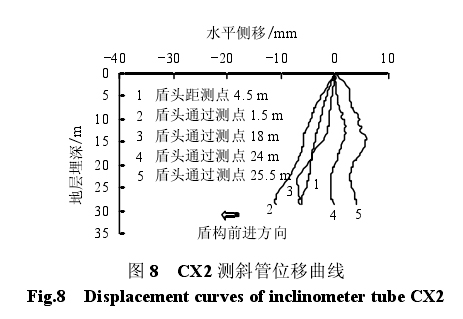
      图 8、9 为盾构在行进过程中，CX2、CX3 测斜管在平行于隧道开挖方向的水平位移变化图。可以看出，距离隧道越远的测点，在隧道开挖影响下水平位移越小，且基本运行规律与 CX1 测点一致，当盾构通过测点的过程当中，水平位移达到最大值，之后由于盾构千斤顶的后推力使得土体呈现出回缩趋势，通过 25.5 m 后仍然回缩，说明盾构机离开测点 25.5 m 后对土体的纵向水平位移扰动仍旧在起作用，纵向位移扰动不可忽略。

      本文采用有限元软件 Abaqus 进行参数的选取与修正。模型的具体尺寸为 120 m×100 m×58.6 m。实际衬砌管片环宽为 1.5 m，取每个开挖步所开挖的土体宽度均为 1.5 m；被开挖土体的直径取盾构机的直径 6.25 m。模型中土体单元采用 8 节点减缩积分一阶单元 C3D8R，衬砌单元采用三维厚壳单元S4，土体与衬砌间的相互作用切向采用罚函数接触面摩擦，法向接触作用采用硬接触，即接触面间只能传递压力，当出现拉力时两接触面自动分离；滑移理论采用小滑移；接触中选用混凝土衬砌面为主面，土体围岩为从面。土体本构模型采用扩展 D-P模型，土体各层材料参数取实际土层表 1 所示。

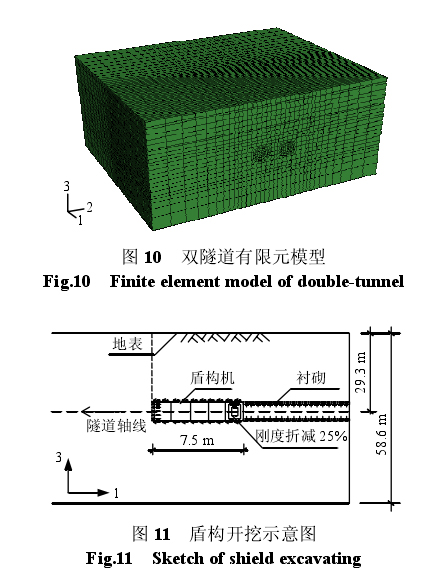
      本文采用刚度折减的方法来模拟开挖过程中盾构机对周围土体的扰动和非及时盾尾注浆所导致的土体应力损失，根据前人经验及实测对比分析，折减系数取 25%。施工现场盾构机通过 ZX2 测点正下方时，开挖面支护压力表读数为 0.3 MPa，盾构机对土体围岩的切向摩阻力为 40 605 N/m²，盾尾均布注浆压力为 0.035 MPa，将上述作为有限元参数。采用数据输出反向导入法进行地应力平衡。有限元模型如图 10 所示，其中，1、2、3 方向分别指平行于隧道开挖方向、垂直于隧道开挖方向、竖直方向。在本试验场地的隧道左线测量中，隧道右线进度快于左线 150 m，即：在试验开始时，隧道右线已经过测点 30 d，可认为初始沉降即将完成。因此，在具体的模拟过程中，先将隧道右线单元杀死，在此基础上再进行地应力场平衡。隧道开挖的实际模拟过程为：隧道右线的开挖、初始地应力场平衡、盾构机体的进入、掌子面力和侧向摩阻力的施加、工作面的开挖、衬砌环拼装、盾尾同步注浆等几个步骤，盾构开挖示意图如图 11 所示。

      图 12～17 为土体水平位移模拟值与实测值的对比，仍旧采用地面点为不动点，其位移对比曲线为相对于管口的水平位移。

      图 12 为 CX1 测管在盾头通过测点 25.5 m 时，沿垂直于隧道方向产生的水平位移曲线，在盾构通过之后，压力注浆作用明显，隧道周围土体在压力注浆作用下向外排开，隧道轴心处土体水平位移最大，达到 20.93 mm，现场实测值为 20.21 mm，当埋深小于 18 m 时，压力注浆作用显著减小。

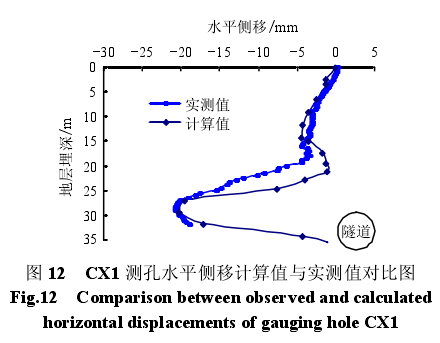
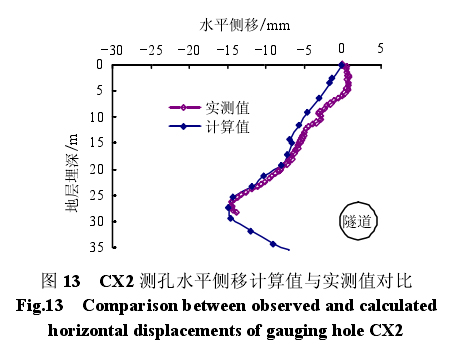
      图 13 为 CX2 测管在盾头通过测点 24 m 后，沿垂直于隧道方向产生的水平位移曲线，在盾构通过之后，压力注浆作用明显，隧道周围土体在压力注浆作用下向外排开，隧道轴心处土体水平位移仍然最大，为 14.56 mm，现场实测值为 14.75 mm，水平位移随埋深变浅而逐渐降低。

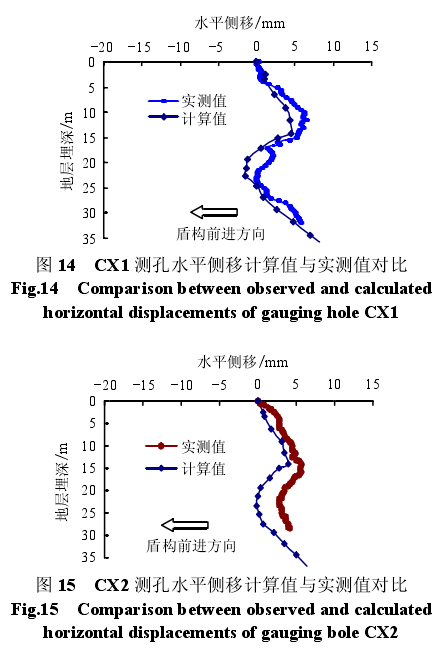
      盾构行进过程中，在盾构到达前以及盾构通过中 U₁方向位移扰动最大，当盾构通过一段距离后，U₁方向位移逐渐回缩。图 14 为盾头通过 CX1 测管25.5 m 后该时刻的水平位移对比图。实测值与模拟值吻合良好，呈现出两个拐点，土体在盾构经过后土体应力损失导致上部土体向后移动，下部拐点在盾构到达前以及通过中产生，又由于盾构通过后在盾构千斤顶的作用下，将衬砌向后挤压，导致衬砌与周围土体向后方摩擦而产生向后的位移。图 15为盾头通过CX2 测管25.5 m后的水平位移对比图，可以明显看出，距离隧道越远，土体位移逐渐减小，CX2 处水平侧移最大值为 5.73 mm，盾构千斤顶引起的下部土体向后方向的水平位移仍然存在。

      盾构在开挖行进过程中，开挖掌子面的推力、盾构与土体围岩的摩擦力、盾尾空隙引起的围岩应力损失、盾尾注浆压力，这 4 部分构成了盾构开挖对土体产生水平位移的主要因素。其中，掌子面推力、盾构与土体围岩摩擦力主要引起平行于开挖方向的水平位移 U₁，盾尾空隙产生应力损失和盾尾注浆压力主要引起垂直于开挖方向的水平位移 U₂。模拟与实测均表明，研究盾构开挖过程中引起的水平位移，横向与纵向均有较大位移，即对于研究隧道开挖引起的土体位移扰动，水平位移 U₁与 U₂均起到极为重要的作用。

      本文取有限元模型第 9 个分析步上的横截面，截取距离隧道轴线上方 6 m 处的竖向路径为研究对象，即与试验中 CX1 测管相对应，重点讨论两相水平位移之间的关系。

      图 16、17 可以看出，在盾头到达测点之前，在开挖掌子面力和盾构与土体围岩摩擦力共同作用下，平行于隧道方向水平位移 U₁沿着开挖方向的变化见图 16，垂直于隧道方向水平位移 U₂沿隧道外侧的变化见图 17；盾头通过测点 3 m 时，U₁位移达到最大值 31.26 mm，此时，U₂位移在盾构开挖引起的应力释放作用下向洞口方向回缩；当盾构通过后，U₁位移开始向后回缩，随着盾尾压力注浆，U₂位移逐渐被排开。

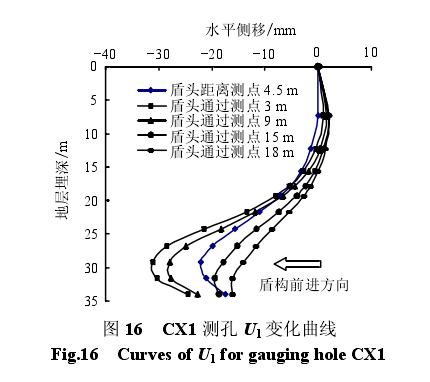
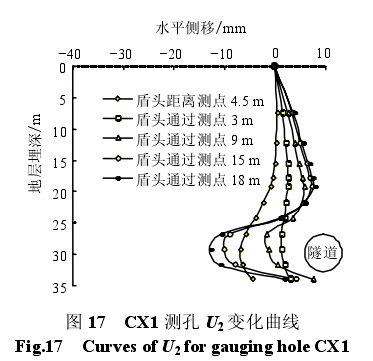
      由图 16、17 还不难看出，在盾构到达前及通过中，U₁位移始终大于 U₂位移，合位移 U 中 U₁占主要成分(U₁与 U₂的矢量和 U 为水平方向的总位移)。当盾构通过后，随着盾构机身与土体围岩摩擦力的消失、盾尾千斤顶力的施加，U₁开始缓慢向后回缩；由于压力注浆的施加，U₂位移开始向外排开，逐渐增大，合位移 U 中 U₂成分越来越多。

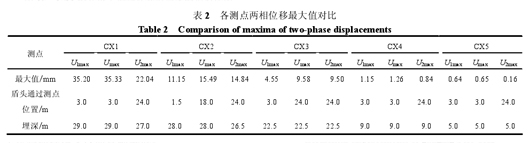
      通过第 2 节实测值不难发现，对于 CX1 测点来说，U₁与 U₂两者的最大值出现的时刻不同，U₁最大值出现在盾头刚刚通过测点 3 m 处，此时盾构机还处于通过测点当中(盾构机身长为 7.5 m)；U₂最大值出现在盾构机通过测点 24 m 处。各测点 U₁、U₂以及合位移 U 的最大值以及产生时间如表 2 所示。

      由表 2 可以看出，距隧道轴线 6 m 处的 CX1测点 U_{1 max}位移大于 U_{2 max}位移，距隧道轴线 12、20 m 处的 CX2、CX3 测点 U_{1 max}位移小于 U_{2 max}位移，CX4 与 CX5 两相位移相差很小。由此也说明，在盾构穿越的总过程中，近隧道区域 U₁位移大于U₂位移，最大合位移 U_max主要由 U_{1 max}来决定；随着与隧道距离的增加，U₁位移的衰减速度大于 U₂位移，最大合位移 U_max中 U_{2 max}的成分越来越多。综上所述，在研究近距离隧道水平位移时，平行于隧道方向的水平位移 U₁应着重加以考虑，尤其是 1倍隧道直径的区域。

      （1）对于垂直于隧道开挖方向土体水平位移U₂，在盾头未到达测点之前，土体向隧道外侧排开；在盾构通过过程中，土体由于应力释放向隧道内侧回缩；当盾构通过测点后，在压力注浆的作用下，土体再次被排开，压力注浆的后期影响作用显著。

      （2）对于平行于隧道开挖方向土体水平位移U₁，在盾头未到达测点之前，隧道轴线方向的土体便开始向前方移动；在盾构通过过程中，土体继续向前方移动；当盾构完全通过后，由于盾构千斤顶作用点在衬砌上，使得衬砌与周围土体围岩发生负横向摩擦，导致土体 U₁方向位移转而向着隧道开挖负方向运动，盾构千斤顶力不可忽略。

      （3）在盾构到达前以及通过过程中，1 倍隧道

洞径区域内，平行于隧道方向水平位移 U₁大于垂直于隧道方向水平位移 U₂；当盾构通过后，U₁位移逐渐回缩，U₂位移开始增大，水平合位移逐渐被U₂成分占据。