摘 要:建立了单轮对的粘滑振动数学模型,考虑了轮对的弹性体模态、轮轨间的蠕滑力—蠕滑率关系在大蠕滑时的负梯度特性、轨道的横向弹性和转向架的一系悬挂特性,分析了多种因素对粘滑振动的影响,研究了波浪型磨耗与粘滑振动之间的关系.通过现场测试获得了与理论分析的一致性.

关键词: 轮轨粘滑振动; 波浪型磨耗; 地铁线路; 曲线轨道

 

      为了从轮轨接触机理上弄清曲线波浪型磨耗形成的机理,在调研了国内外相关成果的基础上^[1-7],建立了细化的单轮对曲线通过数学模型.该模型考虑了轮对的弹性体模态和钢轨的各向刚度和阻尼,采用了与实际情况等效的轮轨蠕滑特性曲线,对多种可能引起轮轨滑动的参数,包括轮对弯曲刚度、扭转刚度、钢轨横向刚度、轮轨粘着水平、运行速度、曲线半径和曲线超高等进行了全面的分析.采用Matlab/Simulink建立了单轮对的曲线通过模型.仿真再现了圆曲线上的轮轨粘滑振动现象.

 

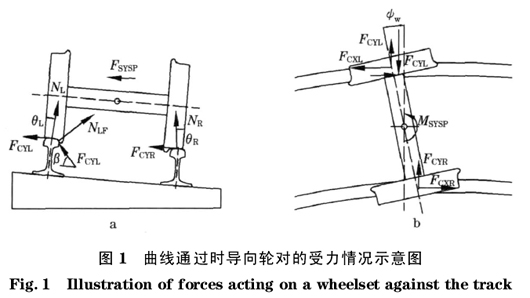
      对于构架式的转向架而言,为了保证一定的蛇形运动稳定性,需要将前后轮对用足够的一系定位刚度与构架相连.当这种转向架通过较小半径的曲线轨道时,过大的定位约束刚度使得轮对很难利用不大的左右轮径差依靠轮轨间的蠕滑导向力使轮对以合理的冲角通过曲线.往往导向轮对以较大的正冲角和较大的横移量以挤压曲线外轨的方式通过曲线,造成轮轨的磨耗.如图1所示为一导向轮在通过曲线时的受力示意图,力的大小和方向与通过小半径曲线时导向轮对的实际情况相符合.虽然采用目前的磨耗型踏面两点接触的可能性很小,但随着轮轨的磨耗,仍然在曲线上容易发生两点接触,或出现共形接触现象,因此示意图中将左轮与外轨的接触看作两点接触,一点在踏面上,另一点在轮缘上.若不考虑回转蠕滑力矩,左侧踏面接触点有两个方向的蠕滑力F_cyL和F_cxL,还有一个正压力N_L.左侧轮缘接触点也有两个方向的蠕滑力F_cyLF和F_cxLF,还有一个正压力NLF.右侧踏面接触点有两个方向的蠕滑力F_cyR和F_cxR,还有一个正压力N_R.左侧轮缘正压力的水平分力远大于左轮上的横向蠕滑力合力,且方向相反.

      本文为了研究波磨机理,仅以单个有一系定位的轮对作为研究对象.以图示力的方向为正方向,根据轮对在纵、横向的静力平衡得:

      F_CYL+F_CYLFcosβ-N_LFsinβ-N_Lsinθ_L+ F_CYR+N_Rsinθ_R=- F_SYSPY                    (1)

      -F_CXL+F_CXLF+F_CXR= F_SYSPX                                                                     (2)

      若不计较小的踏面接触角,式(1)和式(2)即为

      F_CYR= N_LFsinβ-F_CYL-F_CYLFcosβ-F_SYSPY                                                    (3)

      F_CXR= F_CXL-F_CXLF+F_SYSPX                                                                       (4)

      若轮对以平衡速度通过,可以认为F_SYSPY=0,则式(3)为

      F_CYR= N_LFsinβ-F_CYL-F_CYLFcosβ                                                                (5)

      若不计制动与牵引工况,可以认为F_SYSPX=0,则式(4)为

      F_CXR= F_CXL-F_CXLF                                                                                    (6)

      即右侧轮子踏面上的横向蠕滑力为左侧轮缘正压力和蠕滑力在横向方向的合力;右侧的纵向蠕滑力等于左侧踏面与轮缘纵向蠕滑力的合力,大小相等,方向相反.可见右侧轮子上的蠕滑力与左侧轮子上的侧压力和蠕滑力有关;同时右侧轮子上的蠕滑力的合力又受轮轨粘着规律及条件的控制.ψ_w为轮对的冲角.

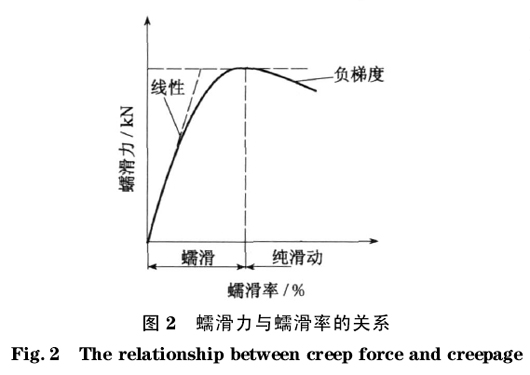
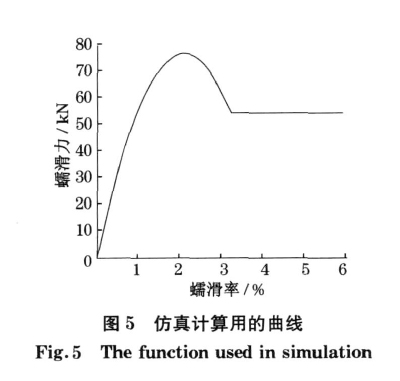
      轮轨间的蠕滑力是蠕滑率的函数,如图2所示.当蠕滑率很小时,它们之间呈线性关系;当蠕滑率较大时,蠕滑力呈饱和特征;当蠕滑率进一步增大时,蠕滑力反而下降,出现负梯度段.当曲线半径较小,而转向架导向性能不良时,左右轮轨接触点很有可能处于这个负梯度段区域.从力学上看,这一负梯度段的作用相当于一负刚度.根据数学分析,这是一个不稳定的系统,即会发生振动发散,由于轮轨蠕滑的强非线性因素,将出现振荡现象.左侧轮子由于轮缘的接触,不可能在轮轨间发生横向的运动,而右侧的轮子处于弹性运动的自由状态,轮轨间有较大的横向间隙和纵向转动弹性体自由度.据此,建立了考虑轮对两种柔体振型的单轮对的动态仿真模型,如图3和图4所示.模型中还考虑了多种可能参与耦合振动的因素,包括轮对弯曲刚度、扭转刚度、钢轨横向刚度、轮轨粘着水平、运行速度、曲线半径和曲线超高等.采用Matlab/Simulink建立了单轮对的曲线通过模型.等效的轮轨蠕滑特性曲线图5所示的曲线表达.

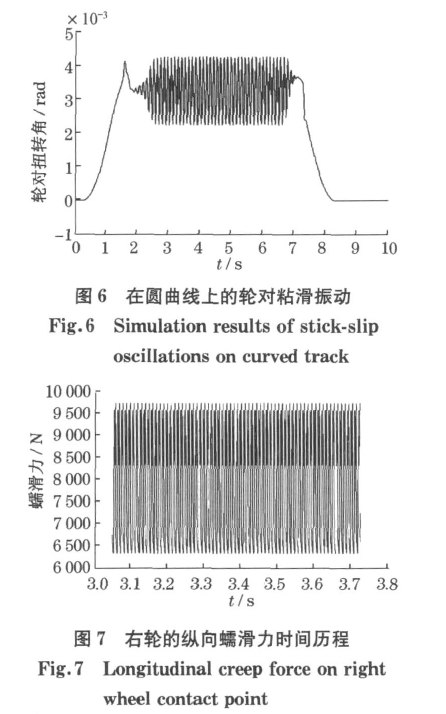
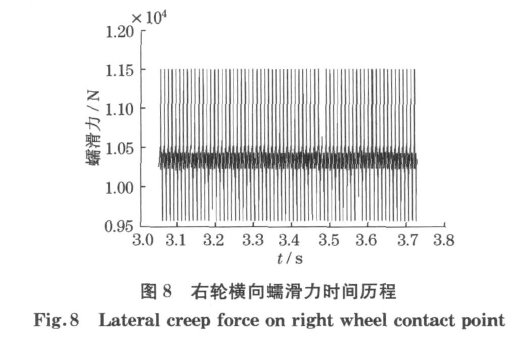
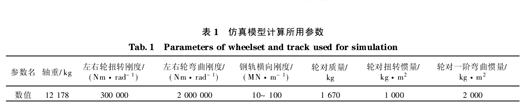
      如图6所示.在特定条件下可以模拟出如图6所示的轮轨间的粘滑振动现象.图7和图8为右侧轮子上的纵横向蠕滑力.一般该振动在缓和曲线的后半段开始发生,在圆曲线上出现稳定的振荡,到出缓和曲线的后半段消失.不同的负梯度,开始出现振动的半径会不同.不同的轨道刚度和粘着水平对振动的产生也有很大影响.通过大量计算分析表明,该粘滑振动的发生规律与现场出现的波磨发生规律相吻合,即这种振动容易出现在曲线内轨的圆曲线上、容易出现在曲线半径较小的区段、容易出现在轮轨粘着条件较好的地下洞内的轨道上、容易出现在轨道刚度较大的整体道床上.表1为仿真时采用的参数.图9为现场曲线内轨上测量得到的有波磨区段的横向加速度信号,可见具有明显的周期振动成份.

      采用仿真软件对几个主要因素进行了多方案的定性分析.主要结果有:影响粘滑振动的首要因素是蠕滑率和蠕滑力之间的负梯度特性,对粘滑振动形成与否有着决定性作用.当蠕滑力饱和后若蠕滑力-蠕滑率特性曲线的负斜率不同,可能产生轮对的粘滑振动的频率也不同.蠕滑力饱和后如特性曲线无下降,无论其它条件如何,均不会发生粘滑振动.其次是轨道的横向刚度和轮对的扭转和弯曲刚度,轨道的刚度低到一定程度就会使耦合振动消失.调查也发现采用木枕的道岔上没有这种波磨,而整体道床的道岔上有严重的波磨.同样轮对扭转和弯曲刚度的减小也会使耦合振动消失.轮轨间的粘着水平对粘滑振动的发生也有影响,计算分析表明,当粘着水平下降时,作用在轮踏面上的合成蠕滑力不容易达到负梯度段,因而粘滑振动不会发生.曲线半径越小会使轮轨蠕滑率越大,使轮轨接触进入负梯度段,发生粘滑振动.现场的调研发现500 m以上的曲线基本没有波磨现象.车辆的一系定位刚度对粘滑振动基本无影响.整车仿真模型的计算也表明,二系悬挂参数对波磨发生也没有影响,因此采用单一轮对研究波磨的是合理的.