基于回归思想的地铁薪酬测算分析
摘 要:随着经济的发展和城市化进程的加快,我国城市轨道交通特别是地铁建设正处在飞速发展阶段。在地铁的建设期间,人员的需求很大,为吸引并留住人才,各城市地铁企业必须制定适应于该城市地铁发展的薪酬体系。分析地铁薪酬测算中的影响因素,并在国内现有城市地铁薪酬方案的基础上,引入多元线性回归的思想构建地铁部门薪酬测算模型,并采用MATLAB软件对该模型进行求解。
关键词:地铁; 薪酬测算; 模型; 多元线性回归
随着我国经济的持续快速发展、城市化进程的加快、政府及国家的大力支持,目前,我国城市轨道交通正处于项目建设与网络化运营快速发展阶段。“十一五”期间国家共投资超过8 000亿元用于城市轨道交通项目建设,截止2009-08已有10个城市建成27条轨道交通线路,运营里程已经超过800 km,此外,已有22个城市的轨道交通规划获国务院批准筹建。城市轨道交通的建设势必带来相应人才的需求,地铁企业吸引并留住人才就需要为员工提供有竞争力的薪酬。较高的薪酬会吸引人才,但同时也会加大城市地铁的人员成本,不利于地铁的建设和发展,因此,必须制定合理的符合城市发展水平的薪酬方案。
1 薪酬影响指标分析
为了克服交通拥堵、环境污染等“城市病”,加快发展以城市轨道交通为骨干的城市客运公共交通系统已经成为共识。但根据测算,地铁每公里造价高达5亿元人民币,而且建成通车后每年还有相当金额的运营成本,投入大、收效慢,巨大的资金压力对地方财政来说是不小的负担。为此,国务院于2003年下达了国办发【2003】81号文件,明确指出城市快速轨道交通系统的建设要“坚持量力而行,有序发展”的原则[1]。虽然影响企业薪酬测算的指标有很多,但基于以上考虑,在地铁部门正职薪酬测算的影响指标主要考虑社会性的指标,并且考虑到城市岗位薪资要与城市规模、人均生产总值、城市居民生活质量相关。因此,选择城市相应的人口规模(常住人口数)、城市GDP以及城市居民人均可支配收入作为影响薪酬的指标。
1.1 城市GDP
GDP即国内生产总值,是宏观经济中最受关注的经济统计数字,被认为是衡量国民经济发展情况最重要的一个指标。城市的GDP高反映该城市经济发展水平较高,对应承担地铁建设的能力也就越强。在城市申报地铁建设的立项条件中依然要求城市的GDP在1 000亿元以上。
1.2 城市居民人均可支配收入
城市居民人均可支配收入是指城镇居民家庭人均可用于最终消费支出和其它非义务性支出以及储蓄的总和,即居民家庭可以用来自由支配的收入。它是城市居民家庭在支付个人所得税、记帐补贴、家庭副业生产支出后所余下的实际收入。
1.3 城市常住人口数
人口规模是在城市地理学研究及城市规划编制工作中所指的一个城镇人口数量的多少(或大小)。一般指一个城镇现状或在一定期限内人口发展的数量,后者与城市(镇)发展的区域经济基础、地理位置、建设条件和现状特点等密切相关。申报建设地铁的城市要求总人口在700万,城区人口在300万以上,才予以立项。
2 基于多元线性回归的薪酬测算模型分析
在现实生活中变量之间的关系是普遍存在的,这种关系一般分为两大类:一类是确定性关系,另一类是非确定关系。其中非确定关系又称为相关关系,而研究变量间相关关系的统计分析方法称为回归分析[2]。
设有p个自变量x1,x2,x3,…,xp(p>1)对因变量Y有影响,他们之间的关系可以用以下模型进行描述
Y =μ(x1,x2,x3,…,xp)+ε. (1)
其中,ε是随机误差,它满足E(ε)=0。基于上述模型的统计分析即为多元回归分析。
当式(1)中μ(x1,x2,x3,…,xp)为线性函数时,便可得到多元线性回归模型
Y =β0+β1x1+β2x2+…+βpxp+ε. (2)
式中:β0为常数项;β1,…,βp为回归系数;ε为随机误差,满足E(ε)=0,Var(ε)=σ2>0;x1,x2,x3,…,xp为确定性变量,Y为可观察的随机变量,β1,…,βp为待求参数。
2.1 薪酬测算模型提取
在地铁薪酬测算中,主要考虑其社会影响指标,分别为城市GDP、城市居民人均可支配收入和人口规模(常住人口数),记为x1,x2和x3,其部门正职的薪酬记为Y,即可得到薪酬测算的模型如下
Y =β0+β1x1+β2x2+β3x3+ε. (3)
2.2 薪酬测算模型求解
在多元线性回归分析中,使用矩阵的使用是必要的,公式(3)可以采用变换称以下表达式
Y = Xβ+ε. (4)
在对模型求解过程中,Yn,xn1,xn2和xn3是已知的,其实就是对常数项β0和系数β1,β2,β3进行求解,人工计算较为复杂,可以通过MATLAB软件的统计工具箱进行计算。MATLAB计算程序如下[3]
x1= [x11 x21 … xn1],
x2= [x12 x22 … xn2],
x3= [x13 x23 … xn3],
A = [x1;x2;x3];a =ones(n,1),
X = [a,A′];Y = [Y1 Y2 … Yn],
[b,bint,r,rint,stats] = regress(Y,X).
程序运行之后可以得到回归系数b=(β0 β1 β2 β3)。
模型求解后,还要对模型的回归显著性进行分析。回归方程显著性分析的方法有很多,结合MATLAB软件的求解,采用判定系数法。判定系数量为R2,公式为
R2=1-Sr/St. (5)
式中:Sr为变量的剩余平方和,St为总偏差平方和。
显然0≤R2≤1,当R2接近于1的时候,说明数据拟合好,即线性回归效果显著,反之当R2接近于0时,说明数据拟合不好,线性回归效果不显著。R2是变量stats中的一部分,变量stats在模型求解中可以得到。
3 模型实例
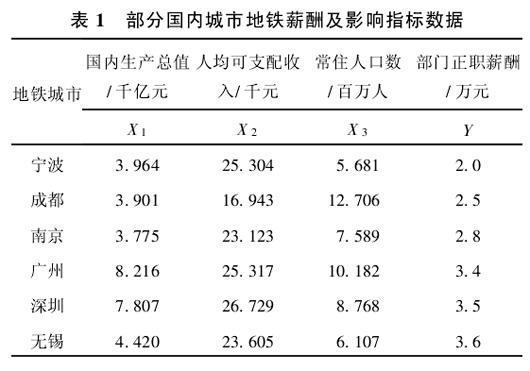
选取国内修建地铁部分城市作为参考,采集各个城市的人口规模(常住人口数)、城市GDP以及城市居民人均可支配收入3个影响指标的数据,并收集各大城市地铁公司部门正职的薪资待遇数据(注:影响指标数据来源于各大城市2008年国民经济和社会发展统计公报)。
通过MATLAB求解程序,得β0=40.101 2,β1=-0.232 4,β2=-0.583 8,β3=-0.246 4,R2=0.864 3,薪酬测算线性回归方程如下
Y =40.101 2-0.232 4x1- 0.583 8x2-0.246 4x3+ε. (6)
R2=0.864 3接近于1,说明多元线性回归方程的显著性较好,适用于计划组建城市地铁公司的薪酬测算方案,其中ε作为地铁薪酬测算中的领导决策区间,可根据各个城市地铁公司的具体情况进行模型修正。
4 结 论
在地铁员工的薪酬测算中,结合多元线性回归思想构建其测算模型,并通过MATLAB编程进行模型求解。针对我国部分修建地铁的城市进行数据回归分析,并计算出适用于计划组建城市地铁公司的薪酬测算方案的模型方程,对城市地铁公司薪酬方案制定具有一定的指导意义。
参考文献
[1]周晓军,周佳媚.城市地下铁道与轻轨交通[M].成都:西南交通大学出版社,2008.
[2]叶慈男,曹伟丽.应用数理统计[M].北京:机械工业出版社,2004.
[3]陈永胜.多元线性回归建模以及MATLAB和SPSS求解[J].绥化学院学报,2007(6):166-168.
[4]高忠清.企业薪酬管理的现状及注意问题[J].山西经济管理干部学院学报,2009,17(4):4-5.
[5]李强.企业如何建立有效的薪酬管理体系[J].人力资源开发,2006(6):34-36.
[6]刘婧,刘晖.关于企业激励型薪酬体系设计的思考[J].沈阳航空工业学院学报,2009,26(6):21-23.
[7]李琪.实施激励型薪酬管理的探讨[J].经济与管理,2004(5):45-46.
[8]陈思明,秦伟平.现代企业薪酬管理中的"球体"理论与实践[J].重庆工商大学学报,2004(1):85-88.