摘  要：利用有限元软件 ABAQUS，采用对隧道洞室周边及开挖面的土体施加由盾构机引起的各种荷载的方法模拟天津市地铁 1 号线盾构施工。计算结果表明，有限元模型能够很好地模拟盾构施工过程。利用此模型研究隧道开挖对桩基础的影响。隧道开挖引起的桩顶沉降、桩身侧移主要发生在盾构机推进面逐渐接近桩的过程中，当盾构机推进面通过桩所在的位置后桩顶沉降、桩身侧移增加不明显；与隧道水平距离相同时，由于长桩能够充分发挥桩身下部的侧摩阻力，隧道开挖引起的长桩的桩顶沉降小于短桩的桩顶沉降；隧道开挖过程中 12 m 长桩的桩身发生了整体倾斜，16、19 m 长桩的桩身出现了弯曲变形，16、19 m 长桩的桩身最大弯矩发生在地面下 12～13 m 之间，即在隧道轴线附近；开挖过程中桩顶出现沿隧道推进方向的往复位移；桩顶作用的竖向荷载越大，由隧道开挖引起的桩顶沉降越大。

关键词：盾构法；隧道开挖；桩-隧道相互作用；桩身侧移；桩侧摩阻力

 

      盾构法具有不影响城市地面交通，噪音、振动小，施工不受风、雨等气候影响等优点，在土质差、水位高的地区被广泛采用，如上海明珠线 2 期、南京地铁 1 号线及天津地铁 1 号线等。

      盾构法施工主要分为3个阶段^[1]。第 1 阶段是土体开挖阶段：通过盾构机前端的全断面切削刀盘的旋转来切削开挖面的土体。第 2 阶段是衬砌（管片）拼装、注浆阶段：盾构机向前推进一定长度（即衬砌或管片的宽度）后，可以进行衬砌（管片）的拼装及盾尾注浆。此时，由于盾构密封舱的脱离，隧道洞室表面的土压力主要由从盾尾向衬砌环外围进行注浆的注浆压力来平衡。第 3 阶段是盾尾脱离阶段：填充在衬砌（管片）和土层间的注浆材料逐渐凝固，强度不断增加。

      许多学者对盾构法开挖隧道对桩基础的影响进行了数值分析^[2–10]。目前，大多数学者采用支撑力折减法或刚度折减法来模拟盾构施工，这两种方法存在以下不足。

      支撑力折减法获得支撑力的土体模型与实际的土体模型有一定差异。图1(a)为获得支撑力的土体模型，隧道对应部分的土体要先被“挖掉”，然后在此基础上建立初始地应力场；而实际开挖中，在建立初始地应力场时隧道对应部分的土体是存在的，见图1(b)。支撑力折减法假定隧道周边的土体位移为，建立的初始地应力场与土体实际的初始地应力场是有差别的。当隧道埋深较大时，这种假定会导致建立的初始地应力场不准确，这是支撑力折减法无法解决的问题。

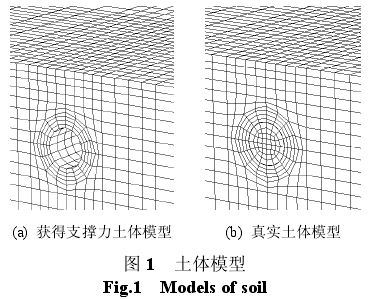
      刚度折减法主要是对开挖部分的土体的刚度进行不同程度的折减来模拟开挖过程中土体应力释放过程。刚度折减法的折减系数取值具有一定的经验性，不同的模型折减系数差别较大。

      本文采用的模拟隧道开挖的方法与上述两种方法完全不同，即通过对隧道洞室周边及开挖面的土体施加由盾构机引起的各种荷载来模拟盾构施工过程。荷载主要有：推进面土体上的压应力（模拟盾构机的推进力），隧道洞室周边的剪应力（模拟盾构机推进过程对周边土体的摩擦作用），隧道洞室周边土体的均布压应力（模拟盾尾的注浆压力）。采用这种方法建立的有限元模型与盾构施工时的真实土体模型相同，而且不需要做任何假定，得到的计算结果能够更真实地反映土体开挖的实际情况。按照这种方法，本文采用有限元软件ABAQUS对天津市地铁1号线盾构施工过程进行模拟^[2]。在此基础上研究隧道开挖对桩基础的影响。

 

      天津市地铁 1 号线^[2]土体的摩擦角、黏聚力、压缩模量 E_s及土层分布见图 2。为了简化计算，图2 将文献[2]中相邻且性质相似的土层合并为一层，相应的土层参数按照各土层厚度加权平均。

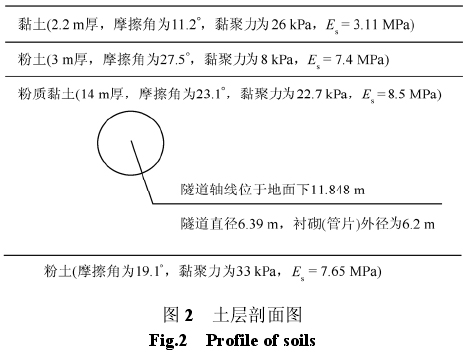
      剑桥模型能够很好地模拟开挖过程中土体卸荷的行为，本文土体采用修正剑桥模型（modified critical state（clay）plasticity model）。由于文献[2]没有提供剑桥模型的相关参数，本文依据土体的类型、压缩模量及土层深度，参考天津市其他工程相似土质条件的剑桥模型参数，初步确定各土层的λ 、k、M 值，通过调整这 3 个参数使有限元计算结果与现场实测结果一致，反演得到各土层的最终参数λ 、k、M 值，见表 1。

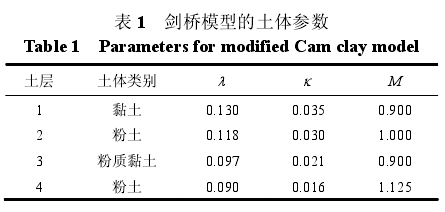
      土体为三维模型，长120 m（沿隧道轴线方向，中间40 m为开挖长度，两侧各40 m为开挖部分与土体边界的距离），宽100 m（隧道中心线距两侧土体边界各50 m），高90 m。土体有限元模型见图3。土体顶部不受任何约束，4个侧面限制与该面垂直方向的位移，底部限制竖向及两个水平方向的位移。

      衬砌（管片）外径为6.2 m，管片厚0.35 m，每环衬砌由6个C45混凝土预制管片拼接而成，衬砌环宽1 m，衬砌管片间由高强螺栓连接。

      将衬砌作为弹性材料。考虑到衬砌（管片）间连接方式导致衬砌变形不连续，姜忻良^[2]将衬砌刚度折减0.15。张志强^[3]取衬砌（管片）刚度折减系数分别为0.75和0.85。本文将C45混凝土的弹性模量折减0.15，取衬砌的弹性模量为2.85×10⁴MPa，泊松比为0.2。

      一般将盾构机的推进力设置为总推力的1/3^[6]。对开挖土体表面施加均布荷载150 kPa模拟推进力。

      模拟隧道开挖时，不同开挖步长对计算结果的影响较小^[4]。为了节省计算时间，本文取盾构机向前推进的步长为4 m，开挖10步，共开挖40 m。

      通过ABAQUS的单元生死技术模拟土体开挖，每个开挖步将一个步长（4 m）的土体挖掉。

      土体被挖掉同时，在隧道洞室周边土体上同时施加均布剪应力及压应力，分别模拟盾构机与土体间的摩擦力及盾尾的注浆压力。

      一般盾构机与土体的摩擦力取为推进力1/10^[6]，本文取施加的剪应力为 15 kPa。

      盾尾注浆是通过 4 个注浆孔注入衬砌（管片）和土层的空隙内，4 个注浆孔的注浆压力不相等，底部两个注浆孔的注浆压力为0.3 MPa，顶部两个注浆孔的注浆压力为0.05 MPa^[2]。虽然底部两个注浆孔的注浆压力比较大，但是它的影响范围是有限的，如果对整个隧道周边的土体施加0.3 MPa的注浆压力，这与实际情况会有很大的差别。姜忻良在隧道洞室周边土体上施加均布压力0.05 MPa模拟盾尾同步注浆^[2]，得到的土体沉降比实测结果略大。参考文献[2]的取值，本文模拟中取均布注浆压力为0.07 MPa。

      利用单元生死技术使9.5 mm厚的注浆层生成。注浆层与隧道土体之间的摩擦力很小，为了节省机时，本文模拟中注浆层与土体之间采用“tie”的连接方式。

      李围^[1]取注浆材料的弹性模量为其所处土层土体压缩模量的1/5。本文取注浆材料的弹性模量为图 2 第 3 层粉质黏土的压缩模量的1/5，为1.7 MPa，泊松比为0.4。

      通过ABAQUS的单元生死技术使对应一个开挖步长（4 m）的衬砌生成，同时取消在隧道洞室周边土体上施加的摩擦力及注浆压力。注浆层与衬砌之间采用“tie”的连接方式。

      注浆材料逐渐凝固，强度不断增加。此时注浆材料的弹性模量取为注浆阶段的10倍^[6]，为17 MPa，泊松比为0.28。

 

      ZX1 是分层沉降仪，位于隧道轴线正上方，与北端头井距离为 12 m^[2]。图 4 为开挖过程中 ZX1测点的沉降曲线。为了表达清楚，图 4 只绘出开挖面距测点 ZX1 为-4～20 m 的沉降曲线，忽略测点沉降变化较小的阶段。

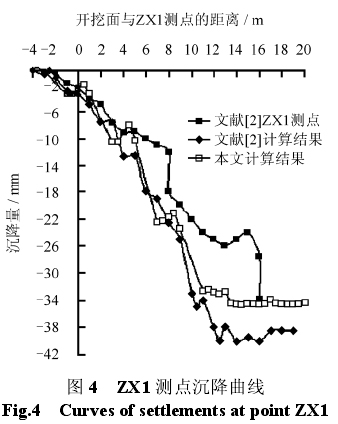
      如图4所示，在开挖面距离测点ZX1为-4～4 m时，两个有限元计算结果与实测结果比较接近。开挖面距离测点 ZX1 为 4～10 m 时，有限元得到的沉降量比实测值大，两个有限元计算得到的沉降量比较接近，只是本文得到的最终沉降量比文献[2]的最终沉降量小 4 mm 左右。这是由于本文采用了与文献[2]不同的土体模型及模拟盾构施工的方法。

      导致现场实测与有限元计算结果存在差异的原因比较多，现场的土质条件远比模型中的土层复杂得多，同时施工方法、仪器测量还受到环境及人为等因素的影响。例如，实测曲线在开挖面距离测点16 m 处沉降量突然增加，这显然是受到了这些因素的干扰，所以有限元得到的结果很难与现场实测完全吻合。

      本文得到的沉降曲线，每开挖一个步长时沉降量会先减小，这是在开挖面的土体上施加推进力导致的。采用“支撑力折减法”及“刚度折减法”是不能反映盾构施工时土体这一变形特点的。

      CX1 是测斜仪，距离隧道轴线 6 m^[2]。图 5 为开挖面通过 CX1 测点 9 m 时地面下各点的水平位移，并假定地面的水平位移为 0。

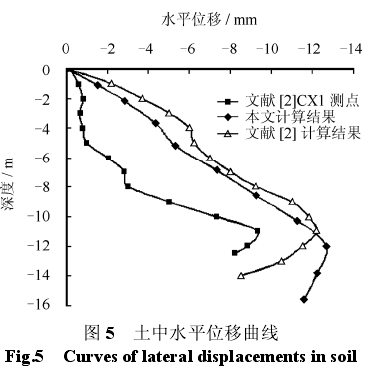
      如图 5 所示，两个有限元计算的结果比较接近，相同深度处计算的位移比实测值偏大 2～4 mm。3条曲线的总体趋势基本上是一致的。

      总体来说，采用本文的参数及模拟方法能够较好地模拟盾构施工过程。

      图 6 为隧道开挖 32 m 后隧道纵断面上土体位移等值线图。图中位移正值表示土体回弹量，负值表示土体的沉降量。北端头井位于坐标零点处。隧道周边局部范围内土体位移出现波浪式起伏，这是开挖过程中在各开挖面土体上施加的推进力引起的。由于推进力只对开挖面附近的土体产生影响，完成 32 m 开挖后，前面 16 m 范围内土体位移的波浪式起伏已消失。开挖导致隧道下方土体回弹，地面下 24.2 m 处土体的最大回弹量为 7.330 mm。

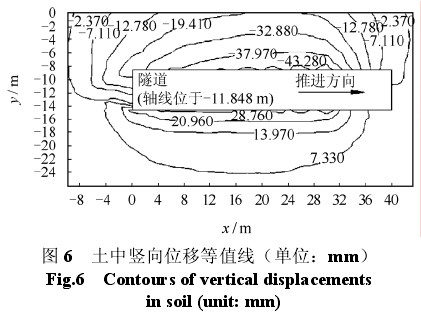
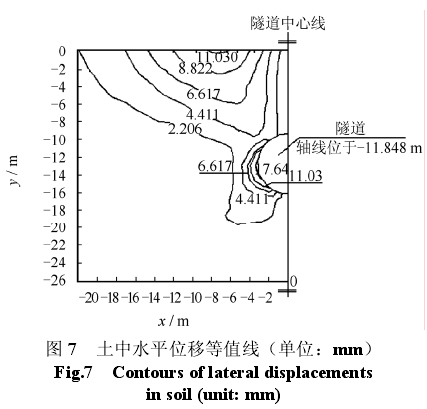
      图 7 为距离北端头井 12 m，当开挖面通过此处8 m 时，隧道周边土体的水平位移等值线图。土体水平位移关于隧道中心线是左右对称的，左、右两侧土体均向着隧道方向水平运动，图 7 只绘出隧道左侧土体水平位移等值线。

      图 7 中地表土体最大水平位移发生在隧道中心线两侧各 7.0 m 处。由水平位移为 2.206 mm 的等值线可以看出，开挖导致隧道中心线一侧土体受扰动的水平范围为隧道中心线以外 23 m，约为隧道直径的 3.5 倍。开挖导致隧道轴线下约 6 m 范围内的土体向隧道方向水平移动。

      桩为直径 0.5 m 的预制桩，采用 C30 混凝土，弹性模量为 3×10⁴MPa，泊松比为 0.2。桩、土之间采用库仑摩擦（Coulomb friction）模型，接触面间的摩擦系数为 0.2。

      在桩顶逐级施加竖向荷载至桩的工作荷载（即桩的极限承载力的 1/2），保持桩顶竖向荷载不变进行盾构法开挖隧道，研究隧道开挖引起的桩顶沉降、桩身变形、弯矩及桩侧摩阻力的变化。

      本文研究了隧道开挖对不同长度桩的影响，桩与隧道的位置关系见图 8。桩与隧道中心线的距离D₁均为 8 m，桩长 L 分别为 12、16、19 m。桩与开挖端头井的距离 D₂均为 18 m，盾构开挖步长为4 m，即桩位于隧道第 5 步开挖土体的右侧。

      桩长不同时其极限承载力不同。本文对桩长分别为12、16、19 m的3根桩逐级施加竖向荷载，获得各自的荷载–桩顶沉降曲线，取曲线转折点处的荷载为各自的极限承载力。桩长为12、16、19 m的3根桩的极限承载力分别为430、640、1 020 kN，相应的各自工作荷载分别为215、320、510 kN。

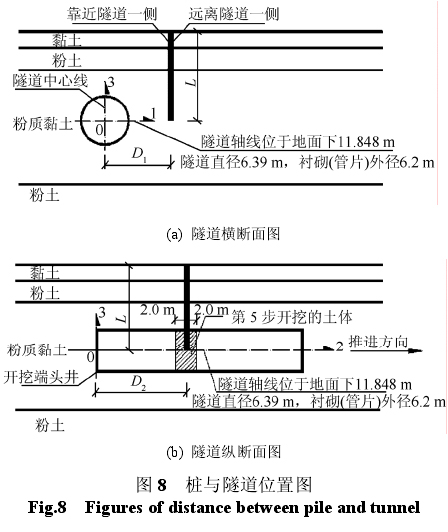
      图 9 为加载及开挖过程中不同长度桩的桩顶及桩底沉降曲线。图中横坐标0～3阶段为逐级施加工作荷载时的桩顶沉降，4～13阶段为隧道开挖过程引起的桩顶沉降。开挖面接近桩的过程中，桩顶沉降逐渐增加。当开挖面通过桩后，如第 6 个开挖步以后（图中横坐标9对应第 6 个开挖步），桩顶沉降基本保持不变。对于12、16、19 m长的桩，由隧道开挖引起的桩顶沉降分别为10.8、8.5、7.5 mm。随着桩长增加，开挖引起的桩顶沉降减小。

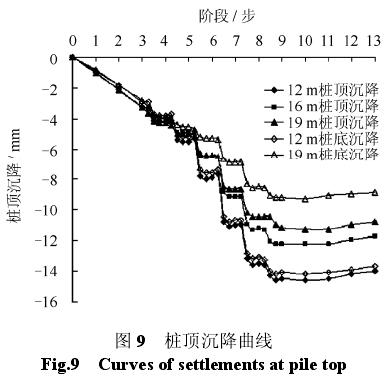
      12 m长桩的桩顶与桩底的沉降量十分接近，这说明12 m长桩的桩身压缩量较小，桩整体下沉。19 m长桩的桩顶与桩底的沉降差为2 mm，即桩身压缩量为2 mm。

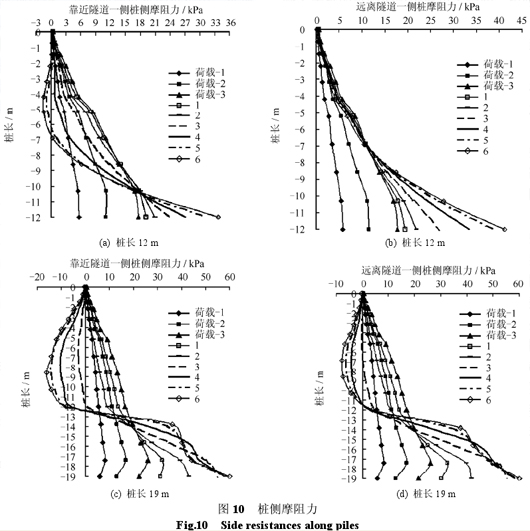
      图10为加载及开挖过程中12、19 m长桩的桩侧摩阻力分布图。由于第6个开挖步以后桩侧摩阻力的变化非常小。为了表达清楚，图10只给出了 3 个加载步及前 6 个开挖步（图10中1～6）的桩侧摩阻力。

      如图10(a)、(b)所示，在加载过程中，12 m长桩的两侧摩阻力随着桩顶竖向荷载增加而增加。开挖过程中，靠近隧道一侧（位置见图8(a)）受到土体侧向卸荷的影响较大，地面下10 m范围内的桩侧摩阻力逐渐减小，第 5 个开挖步后桩上部一定范围的桩侧摩阻力为负值。桩顶竖向荷载不变，上部桩侧摩阻力减小，桩身下部必然要发挥更多的正侧摩阻力。远离隧道一侧，由于土的卸荷作用减小，地面下7 m范围内的桩侧摩阻力随着隧道开挖而略有减小，地面下7～12 m的桩侧摩阻力明显增加。

      对于19 m长的桩，靠近隧道一侧地面下12.5 m范围内桩侧出现了较大的负侧摩阻力。例如，第 6个开挖步时，桩侧摩阻力达到了-16 kPa。竖向荷载作用下桩顶下沉，桩侧土体由于隧道开挖卸荷也会产生沉降。当土体沉降大于桩的沉降时，桩侧出现负侧摩阻力。开挖引起的土体沉降是相同的，但桩长不同，开挖引起的桩的沉降不同。如图 9 所示，19 m长桩的桩底沉降约为 9 mm，小于12 m长桩的桩底沉降 13.5 mm。因此，19 m长桩的桩侧土体沉降大于桩的沉降的范围要更大一些。相应的19 m长桩桩侧负侧摩阻力的范围较大。同样由于这个原因，在远离隧道一侧，19 m长桩地面下12 m范围内也出现了较大的负侧摩阻力。

      19 m长桩下部也必然要发挥出更大的正侧摩阻力以承担桩顶竖向荷载及负侧摩阻力引起的荷载。

      桩与隧道轴线间的距离相同，尽管桩身上部均受到土体卸荷的影响，但由于长桩能够充分发挥桩身下部的侧摩阻力，故长桩的桩顶沉降小于短桩的桩顶沉降。

      在地面下14～17 m范围内，19 m长桩的侧摩阻力出现“台阶”，而不是随着深度增加线性增加。这是由于开挖导致此范围内土体回弹，土中竖向应力减小，土体能提供的侧向土压力减小而导致的。

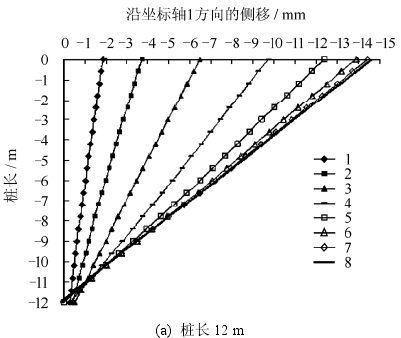
      图11为开挖过程中，不同长度桩沿坐标轴1方向的侧移，坐标轴1方向见图8(a)。图例中数字1～8表示相应的开挖步。图11中桩身侧移为负值表示桩发生了与坐标轴1方向相反的侧移，即桩身向着隧道移动。由第9、10开挖步引起的桩身侧移很小。为了表达清楚，图11只给出了前8个开挖步引起的桩身侧移。

      隧道开挖过程中桩身逐渐向着隧道移动。桩长为 12 m 时，由前 5 个开挖步引起的桩顶侧移为-12.4 mm，约为桩顶总侧移（-14.5 mm）的 86%。当开挖面通过桩后，随后的 5 个开挖步引起的桩顶侧移仅占桩顶总侧移的 14%。这说明隧道开挖引起的桩顶侧移主要发生在推进面逐渐接近桩的过程中，当推进面通过桩所在的位置后开挖引起的桩顶侧移较小。

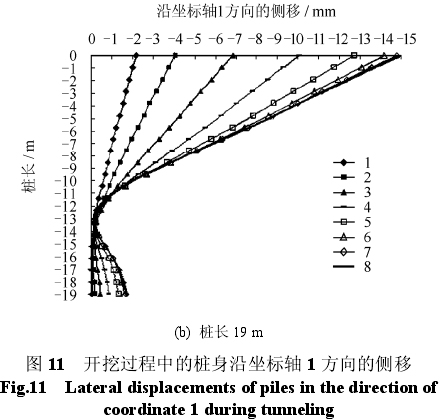
      隧道开挖过程中，12 m 长桩发生了整体倾斜，在完成 2 个开挖步后 16、19 m 长桩出现弯曲变形，反弯点位于地面下 13 m 附近。由于篇幅限制，在此没有给出 16 m 长桩的弯曲变形图。

      隧道开挖引起桩周围土体侧向移动，导致桩侧土压力减小，桩发生侧向移动，即桩身侧移与土体的侧向移动有密切关系。隧道开挖引起土体侧向移动的大小及范围见图 7。由图可知，土体侧向移动主要发生在隧道上部一定范围内（地面下 8.6 m 范围内），隧道轴线处及轴线以下土体的侧移较小。图 6 说明隧道开挖引起其下一定范围内土体卸荷回弹。正如前面分析，土体回弹减小了土中侧向土压力，导致桩身下部因土体侧压力减小而产生侧移。

      因此，隧道开挖导致桩顶发生较大的侧移，隧道轴线附近桩身侧向位移接近于 0。16、19 m 长桩的桩身下部向着隧道的移动，桩身出现了弯曲变形。

      图12为隧道开挖过程中不同长度桩的桩身弯矩图。图中弯矩以远离隧道一侧的桩身受拉为正。

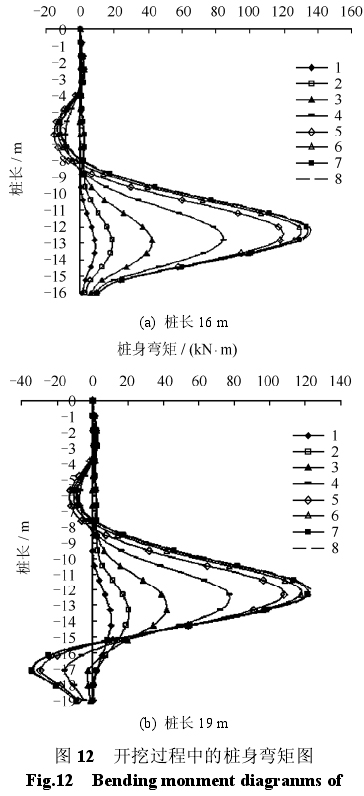
      对于16、19 m长桩，由前2个开挖步引起的桩身弯矩较小，随着开挖面逐渐接近桩，桩身弯矩增加，最大弯矩发生在地面下12～13 m之间，19 m长桩的桩身最大弯矩略小于16 m长桩的桩身最大弯矩。16 m长桩的桩身弯矩曲线出现了两个转折点，19 m长桩的桩身弯矩曲线出现了3个转折点。12 m长桩发生了整体倾斜，桩身弯矩较小，不超过20 kN · m，在此没有给出其桩身弯矩图。

      桩身弯矩与桩身侧移密切相关。地面下14～16 m范围内，16 m长桩的侧移随深度增加而线性增加。地面下14～19 m范围内，19 m长桩的侧移随深度增加而增加的幅度减小，即此范围内19 m长桩的桩身变形又出现了反弯现象，因此桩身弯矩曲线出现了3个转折点。

      通常承担竖向荷载的桩基础设计中没有考虑使桩承担一定的弯矩，仅按构造要求配置一定的箍筋。弯矩作用下桩身混凝土开裂，钢筋锈蚀，影响桩的承载力及稳定性。

      图 8(a)中桩长 L 均为 12 m，桩与隧道中心线的距离 D₁分别取 8、12、20 m。

      计算结果表明：在加载及开挖过程中，随着桩与隧道中心线距离 D₁增加，桩顶沉降、桩身沿坐标轴 1 方向的侧移减小。距隧道中心线为 8、12、20 m时，开挖引起的桩顶沉降分别为 3.1、7.8、14.6 mm。

      图 13 为加载及开挖过程中，与隧道中心线距离D₁分别为 8、12、20 m 时桩顶沿坐标轴 2 方向的侧移，坐标轴 2 方向见图 8(b)。侧移为负值表示桩顶产生与隧道推进方向相反的侧移。

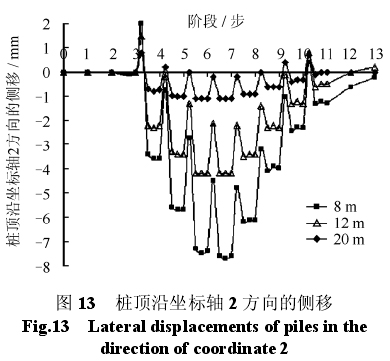
      图 13 中横坐标 0～3 阶段为 3 个加载步，此过程中桩顶不会产生侧移。4～13阶段为10个开挖步，在开挖过程中，桩顶沿坐标轴 2 方向的侧移出现波动，这与开挖过程有关。在一个开挖步中，当对要开挖的土体表面施加推进力时，土体会带动桩沿推进方向（坐标轴 2 方向）运动，例如在第 1 个开挖步中（横坐标 3～4 之间），3 个桩顶沿坐标轴 2 方向的侧移为正；土体开挖时，由于停止施加推进力，同时开挖导致土体侧向卸荷，沿坐标轴 2 方向的土压力同样也会减小，桩顶产生了与坐标轴 2 方向相反的侧移。在整个开挖过程中桩顶不断的沿坐标轴2 方向往复运动，当开挖面远离桩时，土体开挖对桩顶侧向位移的影响减小，桩顶侧向位移逐渐恢复到初始状态。

      计算结果表明，桩与隧道中心线的距离越近，桩受到开挖的影响越大。当距离为 20 m，即为 3D（D 为隧道的直径）时，隧道开挖对桩的影响可以忽略，这与文献[2]是一致的。

      在桩长 12 m，与隧道中心线距离为 8 m 的桩顶上分别施加竖向荷载 215、322、430 kN，模拟桩在1/2 极限荷载（工作荷载）、3/4 极限荷载及极限荷载作用下隧道开挖对桩的影响。

      在相同的开挖步时，桩顶作用不同的荷载时隧道开挖引起的桩身侧向位移基本相同。

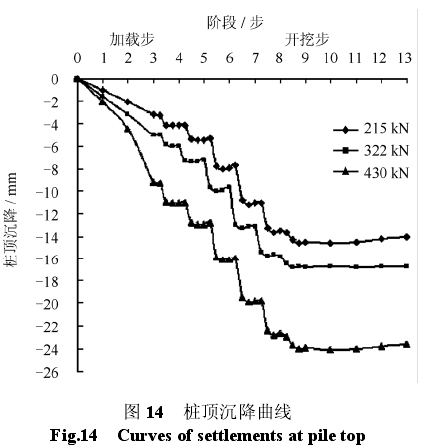
      图 14 为桩顶作用不同荷载时，开挖过程中桩顶沉降曲线。桩顶作用极限荷载、3/4 极限荷载、1/2极限荷载时，由开挖引起的桩顶最终沉降分别为14.4、11.7、10.8 mm。这说明桩顶作用的竖向荷载增加，隧道开挖引起的桩顶沉降增加。竖向荷载接近桩的极限承载力时，桩顶沉降增加明显。

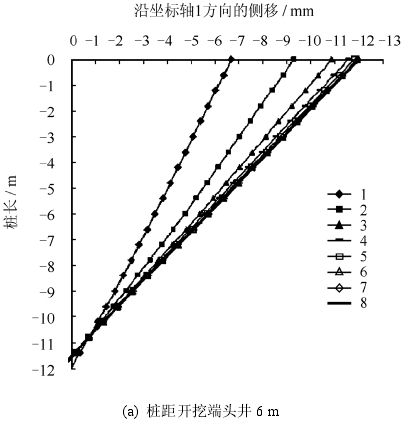
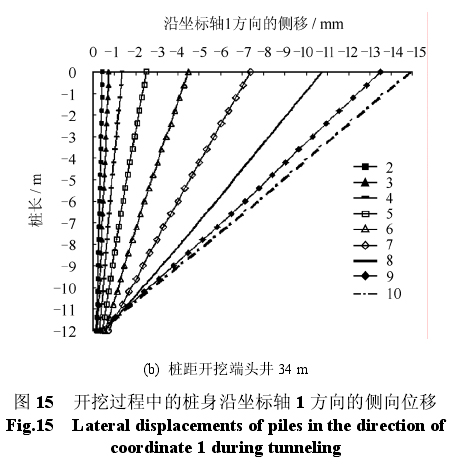
      图 8(b)中，桩距开挖端头井的距离为 18 m，本文还研究桩与开挖端头井的距离分别为 6、34 m 的情况，即桩分别位于第 2、第 9 开挖步的土体的一侧。桩长仍为 12 m、距离隧道中心线 8 m。

      图 15 为开挖过程中桩身沿坐标轴 1 方向的侧移。结合图 11(a)可以发现，距开挖端头井 6、18、34 m 时，推进面接近桩的过程中引起的桩身侧移分别占桩身总侧向位移的 77%、86%、90%。

      当桩距离开挖端头井 34 m 时，第 5 个开挖步完成后桩顶侧向位移不足 3 mm，即当开挖面与桩的距离大于 14 m 时，隧道开挖对桩身变形的影响很小。

      距离开挖端头井 6 m 时桩的总侧向位移比其他两种情况的总侧移小，这是由于桩与开挖端头井的距离比较近，受到推进过程的影响较小。

      采用对隧道洞室周边及开挖面的土体施加由盾构机引起的各种荷载的方法模拟盾构施工，计算结果表明，本文的模拟方法能够较好地反映盾构施工过程。在此基础上研究隧道开挖对桩基础影响，得到如下结论：

      （1）隧道开挖引起的桩顶沉降、桩身侧向移动主要发生在推进面逐渐接近桩的过程中，当推进面通过桩所在的位置后桩顶沉降、桩身侧移增加不明显。

      （2）与隧道中心线距离相同时，长桩能够充分发挥桩身下部的侧摩阻力，长桩桩顶沉降小于短桩的桩顶沉降。

      （3）隧道开挖过程中，12 m 长桩发生了整体倾斜，16、19 m 长桩出现弯曲变形。16、19 m 长桩的桩身最大弯矩发生在地面下 12～13 m，即在隧道轴线附近。

      （4）开挖过程中桩顶出现沿隧道推进方向（坐标轴 2 方向）的往复位移。

      （5）桩顶的竖向荷载越大，开挖导致的桩顶沉降越大。