摘　要:以上海某地铁站与建筑物共建工程为例,现场实测由于地铁运行引起的车站站厅层、上部结构各楼层的动力响应,建立道床—共建结构—地基二维动力有限元模型。通过对比分析计算和实测的共建结构竖向振动加速度的时域谱和1/3倍频程振级谱,探讨普通轨道、科隆蛋高弹扣件轨道和钢弹簧浮置板轨道在引起共建结构振动响应方面的差异。研究结果表明:采用科隆蛋高弹扣件轨道时,共建结构同一位置的加速度峰值约是普通轨道的1/2,而固有频率为6 Hz的钢弹簧浮置板轨道的加速度峰值仅为普通轨道的1/10左右,但钢弹簧浮置板轨道引起的振动周期和持时相对较长;科隆蛋高弹扣件轨道与钢弹簧浮置板轨道均有明显的减振效果,所不同的是前者对25 Hz以下、后者对25 Hz以上频段的竖向振动有较好减振效果;钢弹簧浮置板固有频率的变化对该共建结构振动响应的影响很小。

关键词: 减振轨道; 高弹扣件轨道; 钢弹簧浮置板轨道; 共建结构; 地下铁道; 振动

 

      随着地铁建设的突飞猛进,越来越多地遇到地铁与建筑物共建的大型工程,例如20世纪90年代上海地铁1号线新闸路车站与其上7层办公大楼的共建工程、正在建设的上海自然博物馆和地铁13号线的共建工程等。这类工程除了结构设计复杂、施工难度大以外,需要引起重视的是建成后的地铁在运营中诱发的振动噪声及其处理。

      目前的研究大多限于轨道交通引起的环境振动问题,如夏禾、潘昌实等^[1-3]对城市轨道交通引起的环境振动问题进行了实测和数值计算分析,但未涉及到建筑物和地铁结构共建为一体的振动响应研究。用于轨道上的减振措施包括弹性支承块、高弹性扣件、浮置板轨道等,不同减振措施的减振效果和造价迥异。在共建工程中,由于结构形式、结构刚度差异导致的不同结构固有振动,直接关系到如何选取减振措施。如何在已有经验的基础上,通过理论计算确定出经济合理、技术可行和实际有效的减振轨道结构类型,是摆在诸多学者面前的一大难题。为此,本文以上海某地铁车站及其上部建筑物共建工程为案例,通过实测数据与计算结果的对比分析,分别在时域与频域范围内探讨了普通轨道、科隆蛋高弹性扣件轨道和钢弹簧浮置板轨道对共建结构振动响应的影响规律及其影响程度。

 

　　某已投入使用的共建结构为地铁站与其上部办公楼,地面以下双层结构为地铁车站的站台和站厅层,地面以上的7层混凝土框架结构为某单位的办公楼,整体结构型式并不复杂,各横剖面型式相近,其局部有限元模型如图1所示。车站内采用科隆蛋高弹性扣件轨道结构形式。现场调研表明该地铁车站内无会车情况,列车进出站平均速度最高不超过30 km·h^-1,因此计算时按单向行车、车速30 km·h^-1考虑。

 

      1)测试仪器型号及技术指标现场测试采用的仪器包括:美国NI公司生产的12位分辨率、单通道最大采样频率为200 kHz的PCI (6024E型数据采集卡),国家地震局工程力学研究所研制的891型放大器和891- 型拾振器。

      2)测点布置情况从地铁车站站厅层到办公楼每层楼面均布置有水平和竖向加速度传感器,并逐层拾取有、无列车经过时的振动加速度信号,测点布置如图2所示。

 

      鉴于地铁诱发振动以竖向振动为主的特点,以下重点分析共建结构内的竖向振动加速度。

      测试安排在上午8时至中午12时大楼办公期间进行,并且在每层楼上采集振动数据总时长约30 min,涵盖大约5趟列车进出站的时间,分析时选取振动峰值最大的一组。选取共建结构中地铁车站站厅层和办公楼2层楼面测点的竖向振动加速度结果,根据文献[4]的剥离背景振动技术对其进行背景剥离,获得了单纯由地铁引起的竖向振动加速度的振动数据如图3所示,测点的竖向振动加速度功率谱如图4所示,据此对其进行时域和频域的对比分析。

 

　   1)时域分析

      通过观察测点竖向振动加速度时程曲线可以看出,在列车荷载作用下,竖向振动加速度信号均经历荷载施加、周期性持续和快速衰减的过程,从中不难分辨出测点位置经受6辆编组列车车轮循环冲击时刻以及列车通过后振动衰减的情况,在本实例中1列6辆编组地铁列车循环冲击持续的时间总长约为13 s,地铁进出站的平均车速约在30 km·h^-1,振动衰减较快,不超过0.5 s;另外,各楼层竖向振动加速度的振幅随楼层高度变化而变化,除了站台处因距振源较近其振幅较大外(最大可达0.33 m·s^-2),其他各层竖向振动加速度的振幅变化相差不大,如站厅最大幅值为0.038 m·s^-2, 2楼最大幅值为0.036 m·s^-2。

      2)频域分析

      站台处由于距振源较近,竖向振动加速度主频集中在中高频40~200 Hz范围;其他各层的竖向振动加速度主频主要分布在30~80 Hz范围。站厅和办公楼第2层竖向振动加速度的频谱图如图4所示。

 

 

 

　　为了与高弹性扣件轨道下的实测振动数据对比,通过数值仿真计算,分析假想车站内采用普通轨道与钢弹簧浮置板轨道情况下共建结构内的振动响应。以道床面分界,分别计算道床面上部车辆—轨道耦合动力响应和道床面下部轨下基础的动力响应,然后按照交界面上力协调的原则进行上下部分的耦合运算。

      轨道型式不同,传至道床面(或浮置板支承面)上的轮轨荷载谱(包括荷载大小和荷载波形等)亦不相同。

      对普通轨道来说,以轨道结构底部为交界面, 将普通轨道钢轨上实测轮轨竖向冲击力作为基本输入条件,经过等效处理后再施加到道床—共建结构—地基二维动力有限元模型中。

      对于钢弹簧浮置板轨道,运用车辆—轨道耦合动力学理论^[5],将车辆、轨道和浮置板视为1个相互耦合的振动系统,建立地铁车辆—浮置板轨道耦合振动分析模型。计算出的浮置板轨道下钢弹簧支点的作用力,经过适当修正后即可作为二维计算模型的等效荷载谱。

      以与本实例行车条件(车速和轨道不平顺程度等)接近地段普通轨道钢轨上的实测轮轨冲击力为基本输入荷载(轨腰法测试的轮轨冲击力如图5所示),按照文献[7]认为地铁列车动荷载经钢轨、轨枕传至道床面上时转化为沿轨道中心线均匀分布的2条线荷载进行等效荷载计算。

      F(t) = KnNP(t)/L        (1)

      式中:F(t)为沿轨道中心线均匀分布的线荷载;P(t)为钢轨上实测的轮轨力;n为每辆车的轮对数;N为每列车的编组辆数;L为列车长度;K为分散系数,一般取0.6~0.9^[6],本文取0.7。

 

      采用西南交通大学自主开发的地铁车辆—浮置板轨道耦合振动分析模型,计算不同固有频率浮置板轨道钢弹簧支撑反力谱。

　   在计算模型中,浮置板板长为25 m,板下是2列1.8和1.2 m变间距布置的21根钢弹簧,其中隔振器垂向刚度为6.6 kN·mm^-1,阻尼比为0.05,其他计算参数见文献[9]。通过改变板厚使钢弹簧浮置板固有频率产生变化。行车条件为车速30 km·h^-1,轨道不平顺谱采用美国铁路5级轨道谱,计算结果如图6所示。

      由图6可知:浮置板下的钢弹簧支撑反力是一系列具有一定相位差的激励荷载谱,若欲将其导入到三维计算模型中,则可以按照一系列点荷载输入的方式进行计算,若欲将钢弹簧支撑反力等效地输入到二维计算模型中,则还需以荷载折减方法对钢弹簧的支撑反力进行修正。

      修正模型如图7所示。按图7的模型计算钢轨上作用于地铁列车的不同静荷载组合下钢弹簧支撑反力的分担比,计算结果如图8所示。

 

 

      由图8可见:当钢轨上作用1个轮对时,其下钢弹簧受力的范围小且集中,共有16根钢弹簧受力;当作用1个转向架和2个相邻转向架时,由于临近荷载的叠加与扩散,使得浮置板下钢弹簧分担受力的影响范围变大,分别扩大至24和26根钢弹簧;在此基础上即使再增加其他转向架荷载, 2个相邻转向架荷载下26根钢弹簧的支撑反力也不会受到较大影响。鉴于此,考虑到邻近转向架荷载的相互影响以及不同钢弹簧反力时程曲线的相位差,再经过对上海钢弹簧浮置板路段实例的计算值与实测值对比验证,即可得出二维模型等效荷载的处理办法。

      在固有频率8 Hz、钢弹簧浮置板工况下,不同等效方法得出的地表某观察点计算值与实测值的1/3倍频程频振级谱对比如图9所示。由图9可见,叠合1块浮置板下单侧21根钢弹簧的所有支撑反力与实测值较为接近,因此将其沿该范围长度平均即可作为二维计算模型的外部激励荷载谱。

      局部有限元模型如图1所示,实际模型的左右边界距建筑物边缘为80 m,土层深度为80 m。计算方法采用New mark隐式积分法。

      (1)材料属性。考虑土体在列车振动荷载作用下的剪应变的范围一般在10^-5~10^-4之间,仍处在弹性应变范围内,因此结构和土体统一采用线弹性的力学模型;阻尼按Rayleigh阻尼考虑,在剪应变10^-5~10^-4范围选取阻尼比。

      (2)单元尺寸。单元尺寸与土的剪切波长有关,这里土单元大小取软土地区各土层剪切波长的1/6,即在共建结构和距离振源近处的单元网格长度取0.1 m,而在距离振源远处,沿长度和深度按一定比例放大,但最大网格长度不超过0.4 m。

      (3)边界条件。参照文献[7]的研究,模型两侧采用水平约束,底部采用竖向约束。

      影响结构动力响应准确性的因素除了输入荷载外,还包括材料(土和结构)的计算参数,而材料的动模量、阻尼比无疑是对计算结果影响最大的2个参数。为此,参数的选取主要是通过对现有文献中试验资料收集及相关试验数据分析,并结合已有动力数值分析经验^[8]。

      由文献[6, 9]可知,与地震响应分析不同,地铁运营引起的地基中的振动以中频40~80 Hz为主,所以在计算Rayleigh阻尼系数时,为保证在中频范围内材料的阻尼比在设定值附近,须在中频范围内选择自振频率。

 

 

 

 

 

      由图12可知:   与普通轨道工况相比,科隆蛋高弹性扣件轨道对0~25 Hz频段范围内的竖向振动有较明显的减振效果,分频振级最大可减少20 dB以上(出现在中心频率10 Hz的位置上),但是站厅处和2楼相同位置上的分频最大振级却相差不大,比如在站厅同一观察点,科隆蛋高弹性扣件工况的1/3倍频程最大振级为76.9 dB,比普通轨道工况的80.6 dB仅小3.7 dB;④钢弹簧浮置板轨道对8 Hz以上的竖向振动有明显的减振效果,同样与普通轨道工况相比,不仅分频振级最大可减少30 dB以上(出现在中心频率40 Hz的中高频位置上),而且1/3倍频程最大振级也可减少15 dB左右,但是它却容易放大其固有频率附近的振动能量;(四)通过对比分析科隆蛋高弹性扣件轨道与钢弹簧浮置板轨道的减振效果不难发现,以25 Hz为分界点,对于分界点以上频段的竖向振动,后者优于前者,而对分界点以下频段的竖向振动,则是前者优于后者,可见如若能将它们对不同频段的减振效果取长补短,则有可能在轨道结构上获得1种更为有效的减振综合措施,这是值得进一步研究的课题。

 

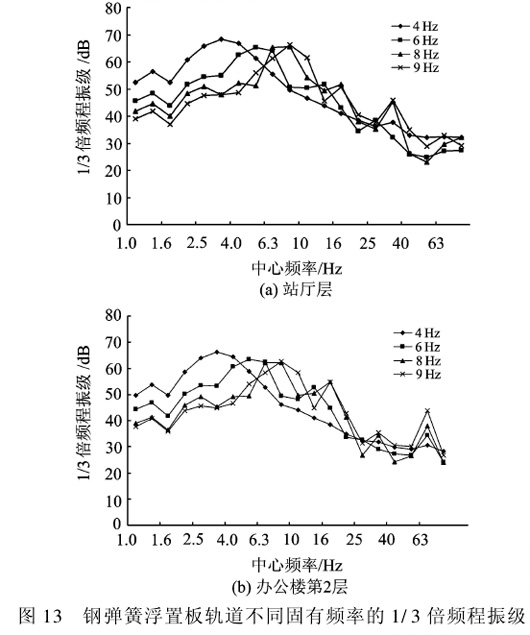
      从图13可以看出,随着钢弹簧浮置板轨道固有频率的降低, 1/3倍频程最大振级向低频移动, 且其幅值也跟着逐渐变大,最大差不超过3 dB,可见,在该共建工程中钢弹簧浮置板轨道固有频率对建筑物的减振影响并不显著,因此,只要选取钢弹簧浮置板的固有频率在4~10 Hz范围内,均可达到相似的减振效果。

      这里要特别指出的是,钢弹簧浮置板轨道固有频率的变化对地铁与建筑物共建结构的影响程度不仅与钢弹簧浮置板轨道的自振特性、钢弹簧支撑反力谱有关,还与共建结构的自振特性有关,因此,不能一概而论。