摘 要: 金属面夹芯板以其良好的吸声降噪性能，被广泛用于声屏障中。而用于高速公路、高架桥道路、城市轻轨地铁以及铁路两侧的金属面夹芯板，则长期受到火车、汽车等经过时所引起的脉动风荷载作用，因此，对其疲劳性能的研究具有重要意义。首先，结合理论分析不同荷载作用下夹芯板能否发生疲劳破坏的几种情况;然后，通过有限元及试验研究验证了理论分析结果。结果表明:理论及有限元分析能反映夹芯板发生疲劳的条件。研究结果指出，由于规格的金属面夹芯板刚度较小，可不考虑脉动风荷载引起的疲劳问题。

关键词: 金属面夹芯板; 疲劳; 理论; 有限元; 试验

 

      近年来，随着工业和交通运输业的迅速发展，噪声污染越来越严重，已危害到居民的生活，而目前采用设立声屏障的方法来治理城市交通噪声不失为一种很好的手段。金属面夹芯板是以上、下两层较薄的高强材料为面板，以相对较厚的轻质材料为芯材，采用一定的成型工艺将两者组合成整体的板材。在实际应用中，将单层面板设计成微穿孔面板，芯材采用玻璃丝棉、岩棉等多孔吸声材料，因此，金属面夹芯板具有良好的吸声降噪性能。同时由于其轻质高强，快捷建造无需起重设备，利于恶劣环境安装，损坏时易修复更换，维护费用低，使用寿命长。因此，目前金属面夹芯板已成为声屏障隔声板的首选。金属面夹芯板中，钢板是常见的面板。

      而用于高速公路、高架桥道路、城市轻轨地铁以及高速铁路等周围的夹芯板，则长期受到火车、汽车等经过时所引起的风荷载作用，因此，夹芯板的疲劳性能也一直受到大家的关注，值得详细研究和探讨。本文结合理论、有限元及试验对夹芯板的疲劳性能进行了研究。

 

      目前，对金属面夹芯板疲劳性能的研究主要集中在国外，国内尚缺乏展开相关研究。国外的研究可分为对芯材疲劳性能和对夹芯板(或层合板) 整体疲劳性能的研究。

      文献［1］对蜂窝和泡沫建立了理论模型，分析发现:芯材中的裂纹扩展速率取决于循环应力密度，孔的大小、密度和原材料的疲劳参数。文献［2］指出，多孔固体材料的性能不仅与原材料有关，还与孔结构有关。文献［3］通过静态试验研究了刚性聚苯乙烯泡沫的断裂，指出线性断裂机理适用于其断裂特征。文献［4］研究了聚苯乙烯泡沫模型 － I 中疲劳裂缝的扩展速率，并采用线性断裂理论对裂缝尖端的应力密度因素进行了计算。

      对板的疲劳性能研究，传统的研究方法大多集中在其刚度^{［5 － 6］}、剩余强度^{［7 － 8］}及其他力学性能的变化来预测试件的疲劳破坏。剩余刚度可以在非破坏的状态下测得，因此是一种简单预测疲劳寿命的方法。文献［5］提出疲劳模量的概念，假设疲劳模量与循环次数及应力水平有关，每次循环中的应力与应变存在线性关系，弹性模量的退化速率与循环次数存在指数关系。这样，经过推导就得到了疲劳寿命与初始模量、失效模量及材料常数之间的关系，并在应变失效准则下，得到了疲劳寿命与应力水平之间的关系。文献［9］采用刚度退化法给出了循环荷载下夹芯组合结构疲劳性能的分析方程，来预测结构的疲劳寿命及疲劳损伤。文献［10 － 11］采用了四点弯曲加载，并采用了正反向加载的试验装置。通过试验得到了不同荷载等级及应力比下的应力 －寿命曲线，并拟合成二参数 Weibull 函数，考察了不同应力水平的影响。文献［12］首先通过试验获得了循环荷载下铝合金泡沫的剪切应力 － 应变关系;然后结合试验结果及理论研究，给出 4 点弯曲单调加载时常见的 3 种夹芯梁破坏模式(金属面板屈服、芯材剪切、芯材压痕)的计算公式。文献［13］对夹芯板 3 点弯曲疲劳加载过程中的裂纹扩展状况进行了研究。

      由上可知，目前国外的研究中大多集中在对小尺寸泡沫芯材夹芯板试件的研究，专注于对夹芯板破坏形式的研究，而不考虑大尺寸构件在正常使用状态的要求。本文拟结合国内对金属面夹芯板的变形要求及其力学性能随振动次数的变化来研究实际应用中足尺寸金属面夹芯板的疲劳性能。

 

      本文以实际应用中足尺寸的金属面夹芯板整体为研究对象，假定芯材与金属面板粘结良好，并由于芯材力学性能的变化对夹芯板承载力影响较小，可不考虑芯材力学性能随振动次数的变化，因此钢材的疲劳性能就决定了夹芯板的整体疲劳性能。

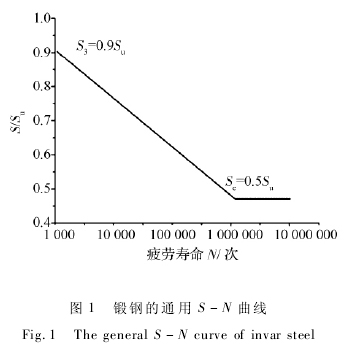
      经过多年的经验积累，钢材的疲劳性能与其拉伸特性之间的经验关系式已经比较成熟，也已成为工程师们评估疲劳性能的重要工具。当不同强度钢材的 S － N 曲线用疲劳极限强度 S_e(即 10⁶次循环时的应力幅 S₆)和极限抗拉强度 S_u绘出时，如图 1所示，所有的曲线都倾向于下式表达的简单曲线:

      S_u< 1 400 MPa 时，S₆= S_e≈ 0. 5S_u             (1a)

      S_u> 1 400 MPa 时，S₆= S_e≈ 700 MPa         (1b)

      钢材在 10³次循环时的应力 S₃可以近似为0. 9S_u。图 1 取大多数时 S_u< 1 400 MPa 的情况。一般认为，钢材的疲劳极限次数为 100 万次。

      根据夹芯板的使用是否会影响结构的安全或产生不利的变形，通常有两个判定金属面夹芯板能否继续使用的准则:1) 承载力极限状态时的强度准则，即此时继续使用试件将影响结构的安全性能;2)正常使用状态的变形准则，即此时变形太大，会影响结构的适用性，在结构中通常以跨中挠度达到板跨长度的 1 /200 为准，即 f≤l/200。试件在荷载作用 下，当 应 力σ = 0. 5S_u时，记 对 应 的 荷 载 为p_{0. 5应力}:当应力σ = S_u时，记对应的荷载为 p_全应力。令试件在荷载作用下跨中挠度达到 l/200，即 f =l /200时，对应的荷载记为 p_变形。结合图 1，荷载作用下的夹芯板会产生以下几种情况。

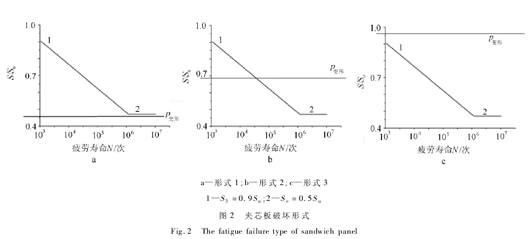
      1)p_变形≤p_{0. 5应力}时，此时静力破坏由变形控制(p_变形)，施加的荷载只能在 p_{0. 5应力}之下，应力强度不会随循环次数而降低，不会发生疲劳破坏，见图 2a。

      2)p_{0. 5应力}< p_变形≤p_应力时，此时静力破坏虽然由变形 控 制 ( p_变形)，但 由 于 施 加 的 荷 载 可 能 超 过p_{0. 5应力}，故有两种可能:施加的荷载在 p_{0. 5应力}和 p_变形之间，应力强度会随循环次数而降低，会发生疲劳破坏;施加的荷载小于 p_{0. 5应力}，应力强度不会随循环次数而降低，不会发生疲劳破坏，见图 2b。

      3) p_应力< p_变形时，此 时 静 力 破 坏 由 强 度 控 制p_全应力，不会发生变形破坏，施加的荷载大于 p_{0. 5应力}，也有两种可能:施加的荷载在 p_{0. 5应力}和 p_全应力之间，应力强度会随循环次数而降低，会发生疲劳破坏;施加的荷载小于 p_{0. 5应力}，应力强度不会随循环次数而降低，不会发生疲劳破坏，见图 2c。

      本文所用试件为深圳安泰科技有限公司生产的高速铁路吸 － 隔音板(ATEC － HR － A1 型)，试件尺寸为长 × 宽 × 高:1 960 mm × 500 mm × 140 mm，上、下层钢板均为 Q235 钢，厚度为 t = 1. 2 mm，中间吸声材料为密度 48 kg/m³的超细玻璃丝棉。拉伸试验测得的上下钢板的极限强度 S_u= 395 MPa。

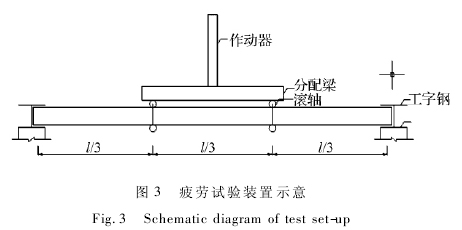
      实际中，近似认为位于高铁两旁的金属面夹芯板受到均布荷载作用，但在试验中，采用目前疲劳试验常用的 4 点弯曲加载方法，在试件对称位置施加2 个相等的集中荷载，使板跨度中段为纯弯曲区域。为了模拟实际中夹芯板的边界条件，在试件两端采用工字钢固定，并在工字钢与试件中间填充橡胶垫，以使试件在端部夹牢固。疲劳试验机作动器通过分配梁与滚轴相连，对试件施加对称等值集中荷载，为了能对试件施加拉压荷载，在试件的上下表面均装有滚轴，如图 3 所示。试验中所施加的荷载通过跨中弯矩相等的原则确定，即令集中荷载作用下的跨中弯矩与均布荷载下的跨中弯矩相等。根据实际中测得的均布荷载为 3. 07 kN/m²，可计算出作动器施加的荷载为 2. 3 kN。

      结合试验中的边界条件及试件状况建立试件的ABAQUS 有限元模型，如图 4 所示。有限元模拟中，钢板采用壳单元 (S4R)，玻璃丝棉采用实体单元(C3D8R)，因为钢板与芯材粘结良好，能保证共同工作，所以采用粘结的方式将两者连接。将支座和中间加载点简化为刚片，以便于设置边界条件。两端支座简化为简支，同时约束其 3 个方向的转动。

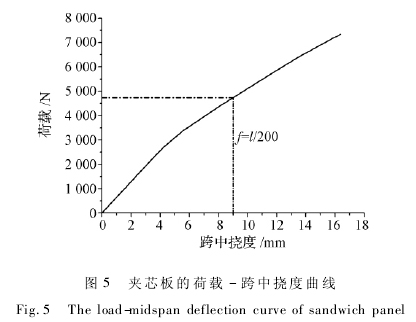
      对试件加载进行静力分析，得到试件的荷载 －跨中挠度曲线见图 5。结合 2. 2 理论分析，可以判断试件是由正常使用状态的变形控制。对试件施加2. 3 kN 荷 载，此 时 跨 中 钢 板 的 最 大 应 力 σ_max≤0. 5S_u，因此判断试件在此循环荷载下不会发生疲劳破坏。

      试验采用正弦循环加载，应力比为 R = － 1，加载频率为 4 Hz，如图 6 所示。要求对试件加载循环438 万次。

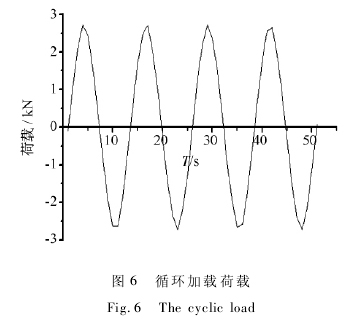
      按上述试验条件，在对试件进行 438 万次循环荷载的过程中，荷载及试件跨中挠度均稳定变化，没有明显增加现象，说明试件受力性能仍良好，即试件没有发生疲劳破坏。

 

      1)结合钢材的通用 S － N 曲线及夹芯板使用过程中的变形或强度要求，分析了夹芯板是否会发生疲劳破坏的几种情况，并验证了分析结果的可靠性。

      2) 对夹芯板的疲劳性能进行了试验研究，同时建立了有限元模型，并将两者结果相比较，两者结论一致。

      3) 实际中常用规格的金属面夹芯板刚度相对较小，通常以变形过大影响结构的正常使用，且在火车高速经过时引起的风荷载作用下，应力水平较低，因此在此循环荷载下不会发生疲劳破坏。

 

［1］ Burman M，Zenkert D. Fatigue of Foam Core Sandwich Beams-1:Undamaged Specimens［J］. Int J Fat，1997，19(7):551 － 561.

［2］ Burman M，Zenkert D. Fatigue of Foam Core Sandwich Beams-1:Effect of Initial Damage［J］. Int J Fat，1997，19(7):563 － 578.

［3］ Huang J S，Lin J Y. Fatigue of Cellular Materials［J］. Acta Mater.，1996，44(1):289 － 296.

［4］ Gibson L H，Ashby M F. Cellular Solid-Structure and Properties［M］. 2nd ed. Cambridge: Cambridge University Press，1997.

［5］ Zenkert D，Backlund J. PVC Sandwich Core Materials-Model Fracture Toughness［J ］. Compos Sci Technol，1989，34 ( 3 ):225 － 242.

［6］ Shipsha A，Burman M，Zenkert D. On Mode-I Fatigue Crack Growth in Foam Cores for Sandwich Structures and Mater［D ］.Stockholm: Department of Aeronautics， Royal Institute of Technology，2000:103 － 116.

［7］ Hwang W，Han K S. Fatigue of Composites-Fatigue Modulus Concept and Life Prediction［J］. J Compos Mater，1986，20 ( 3 ):125 － 153.

［8］ Highsmith A L，Reifnider K L. Stiffness Reduction Mechanisms in Composites Laminates［G］∥ Reifsnider. Damage in Composite Materials. SASTM STP，1982:103 － 117.

［9］ Hwang W，Han K S. Statistical Study of Strength and Fatigue Life of Composite Materials［J］. Composites，1987，18(1):47 － 53.

［10］ El Kadi H，Ellyin F. Effect of Stress Ratio on the Fatigue of Unidirectional Glass Fibre / Epoxy Composite Laminates ［J ］.Composites，1994，25(10):917 － 924.

［11］ El Mahi A，Khawar Farooq M，Sahraoui S，et al. Modelling the Flexural Behaviour of Sandwich Composite Materials Under Cyclic Fatigue［J］. Mater Des，2004，25(3):199 － 208.

［12］ Caprino G，Giorleo G. Fatigue Lifetime of Glass Fabric/Epoxy Composites［J］. Composites Part A. ，1999，30:299 － 304.

［13］ Harte A M，Fleck N A，Ashby M F. The Fatigue Strength of Sandwich Beams with an Aluminium Alloy Foam Core ［J ］.International Journal Fatigue，2001，23(6):499 － 507.