摘   要：洞桩法能够较好地控制地层变形和对周边既有建（构）筑物的影响，目前已成为北京地铁暗挖车站施工的主流工法。以北京地铁 10 号线黄庄站工程为背景，基于地表和管线沉降的实测数据，建立“隧道-管道-土体”的三维有限元计算模型，研究了洞桩法车站施工对地层的影响，并从沉降、变形和管-土相互作用等方面系统研究了施工对邻近刚性接头管道的影响。研究结果表明，洞桩法车站施工中导洞和扣拱施工是关键工序，这两个工序引起的地表沉降占总沉降的 90%以上；刚性接头管道的沉降、变形及管道-土体差异沉降与管道和隧道相对位置关系密切相关，主要受其正下方土体开挖影响；管道变形由整个管体共同承担，地层位移使管道产生弯曲和轴向变形，建议采用应变作为管道变形控制标准。

关 键 词：洞桩法；地铁车站；地表沉降；刚性接头管线；管-土相互作用；施工影响

 

      城市地铁工程大多穿越既有城区，很多情况下不具备明挖施工的条件，暗挖地铁车站的环境风险很高，地表沉降和邻近建（构）筑物变形的控制标准严格。洞桩法吸收了盖挖法和暗挖法的优势，能够较好地控制地层变形和对周边既有建（构）筑物的影响，目前已广泛用于北京地铁工程。

      地铁洞桩法施工对地层变形和管线的影响已有一些研究，刘维宁^[1]等研究了北京地铁复八线天安门西车站暗挖施工对地层沉降以及管线变形的影响。吴波^[2]紧密结合深圳地铁大——科区间实际工程，采用数值模拟和离心机试验方法，系统研究了杂群洞隧道工程施工所引起的地表沉降空间效应和流变效应。李大勇^[3]采用三维有限元法对软土地基深基坑工程邻近地下管线的性状进行了系统研究。王霆等^[4]综述了国内外隧道工程施工对地下管线影响的已有研究成果。何海建^[5]分别从空间效应、时间效应、邻近桥基差异沉降的概率分析 3 个方面探讨了地铁洞桩法施工对邻近桥桩的影响。李兴高等^[6－7]在地层移动基本规律的基础上，提出了一种经验或半经验的基于变形控制的柔性管线的安全评价方法和刚性管线纵向应变计算及安全评价方法。

      地铁车站施工对刚性接头管线的影响研究较少（刚性接头管线是指在保证使用功能的条件下，接头不能或不允许发生转动的管线，典型的刚性接头管比如焊接钢管），本文以北京地铁 10 号线黄庄站工程为背景，在对管-土相互作用合理模拟的基础上，运用数值分析与现场监测数据结合的方法，选取直径为 1 400 mm 的上水钢管作为研究对象，系统研究了洞桩法车站施工对地层和刚性接头管线的影响。

 

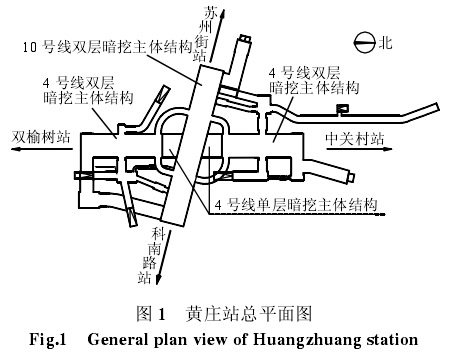
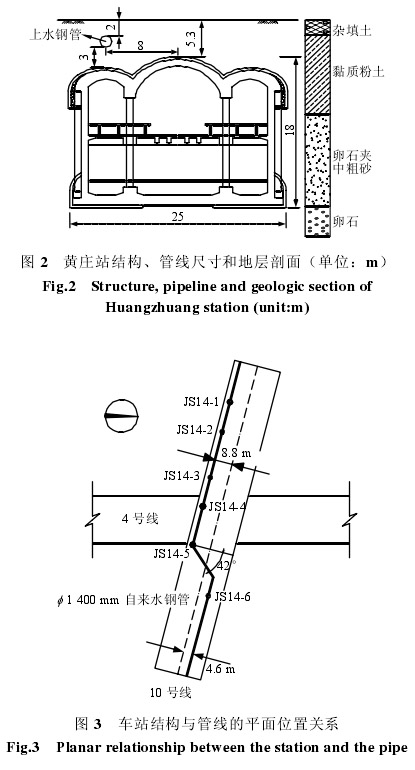
      黄庄站为北京地铁 10、4 号线换乘站，采用洞桩法施工，如图 1 所示。车站上方管线密布，导洞与主体结构上方多处与管线距离很近。管线类型多样、材质各异、剩余承载和变形能力差别较大。车站主体采用洞桩法施工，车站规模大、埋深浅、结构和施工工艺复杂，国内外均属罕见。黄庄站的施工难度和风险很大，对地表沉降和邻近管线的影响问题十分突出。车站结构与管线的剖面位置关系与穿越的主要地层如图2 所示，车站最小覆土为5.3 m，开挖范围内主要穿越粉质黏土、卵石和中粗砂地层。

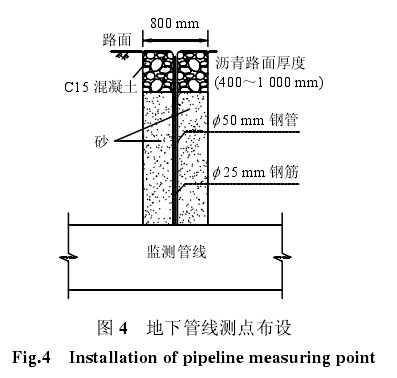
      车站结构与管线的平面位置关系如图 3 所示，管顶覆土为 2 m。共布置了 6 个管线监测点，测点布置方案采用套筒式，如图 4 所示，数值模拟选取典型管线测点（JS14-3）监测数据进行对比分析。

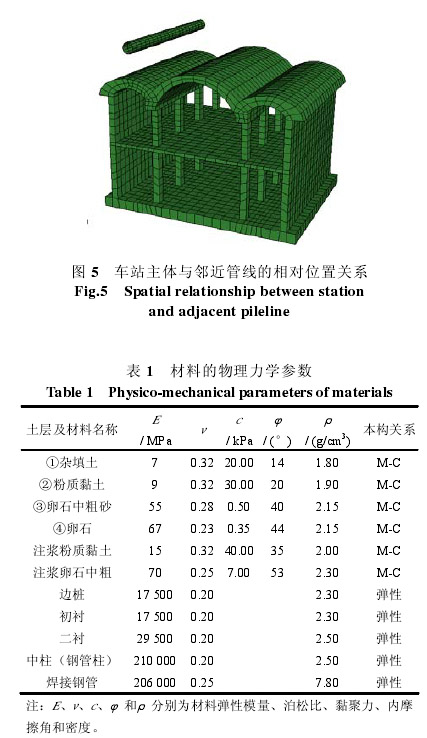
      模型总高度为 35 m，模型宽度取 130 m（约为7D ，D 为主体结构跨度），线路纵向考虑边界效应取 20 m，计算模型网格如图 5 所示。计算采用不同的本构模型模拟不同的材料，对于初期支护、二次衬砌、边桩和钢管等采用线弹性模型，而土体均采用摩尔-库仑（M-C）模型。模型中材料的物理力学参数取值以黄庄站地质勘察资料为基础，如表 1 所示。

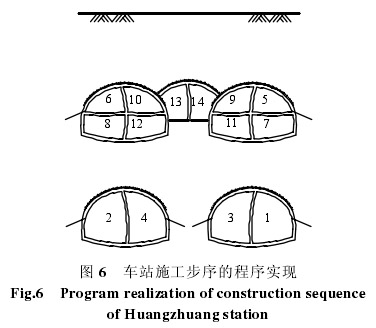
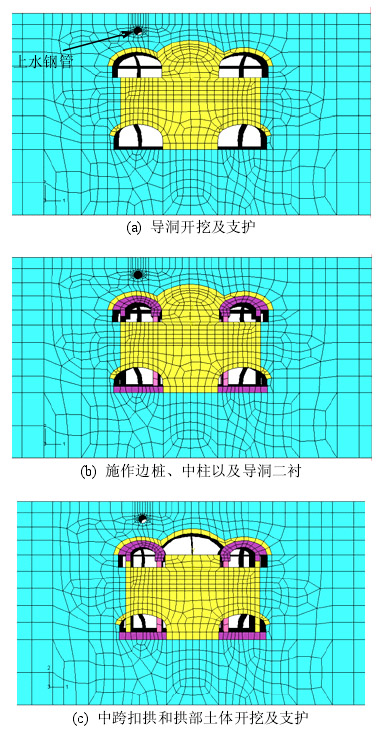
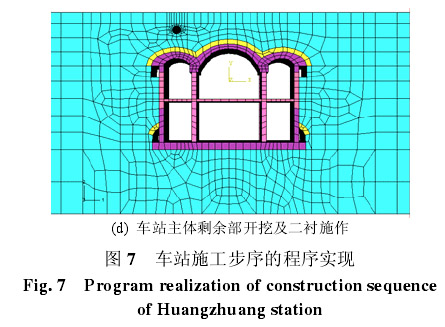
      车站采用四导洞的洞桩法施工，导洞开挖步序如图 6 所示，为更好地控制地层变形，上导洞采用交叉中隔壁法（CRD 法）施工。典型施工步序包括：①导洞开挖及支护（见图 7(a)）；②边桩、冠梁及中间立柱施工，施作导洞二衬（见图 7(b)）；③ 扣拱施工，中跨拱部土体开挖及支护，拱部二衬施工（见图 7(c)）；④开挖至结构中楼板底标高处，施做中板和上层边墙；⑤开挖至底板底，施作底板及下层边墙（见图 7(d)）。导洞和中跨拱部土体每次开挖进尺为 1 m，共分 20 步开挖，相邻开挖步间距为 5 m。

      ABAQUS 程序中主从接触面法可模拟管-土的法向相互作用和脱离以及切向的相对滑移，从而更真实地反映了管-土作用的机制。

      ABAQUS 程序接触分析中，需要确定主面和从面，通常管道外表面设置为主面，周围地层面为从面。主从面接触可模拟管道与土体的法向侵入、脱离和切向的相对滑移，从而更真实地反映了管-土相互作用的机制。接触面的相互作用按照切向和法向分别定义，切向接触时一旦管-土节点发生接触，就不能再发生相对滑动。法向接触中允许管-土节点相互分离。模拟的难点在于接触参数的选取，计算中应根据实际管道及周围土体的性质、管周土体的密实度、管道的埋置深度等因素综合考虑。

      通过试算与分析，最终确定法向接触采用硬接触，切向接触采用罚函数摩擦模型，摩擦系数取 0.3。

 

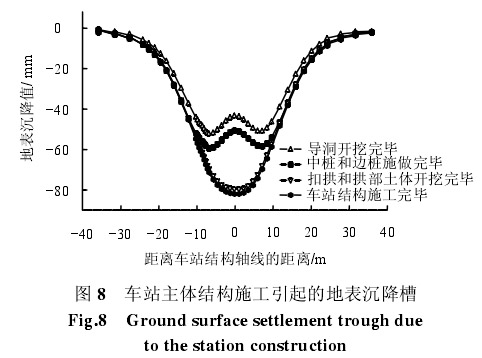
      取模型纵向 10 m 处的横断面为地表沉降的监测断面，各施工阶段的地表沉降槽如图 8 所示。洞桩法施工引起的最大地表沉降在 82 mm 左右。分析表明，洞桩法施工中，导洞开挖支护所引起的地表沉降约占最终沉降的 53%左右；施作边桩、中柱以及导洞二衬所引起的地表沉降约占最终沉降的8.8%左右；中跨扣拱和拱部土体开挖及支护所引起的地表沉降约占最终沉降的 35%左右；剩余的土体开挖，二衬施工所引起的地表沉降约占最终沉降的3%左右。拱部土体开挖和支护完毕后，地表沉降趋于稳定，后续施工在导洞及拱部初支、边桩和中柱的保护下进行，所引起的地表沉降很小。因此，可按前 3 个典型阶段进行沉降控制和分析，前 3 个典型施工阶段引起的地表沉降比例大约为5.5:1.5:4.2。

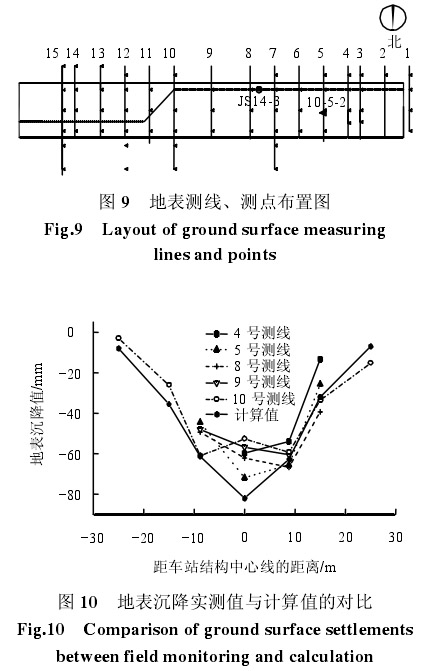
      地表沉降监测数据分析：10 号线黄庄站地表沉降测点布置如图 9 所示，共有 15 条测线，位于管线测点范围内的测线共有 5 条，分别为 4、5、8、9、10 号测线。这 5 条地表沉降测线的最终沉降槽曲线与计算曲线如图 10 所示，从图中可以看出，实测最大地表沉降发生在 5 号测线的 10-5-2 号测点，达到72 mm。管线 JS14-3 号测点位于 8 号测线，最终沉降最大值为62 mm，计算值大于实测值约30%左右。数值计算中选择管道顶部正上方的地表沉降为主要标定值，使得数值计算结果在该处与实际尽量符合，导致了车站轴线正上方的地表沉降计算结果偏大。

      实际施工中，①导洞开挖和支护、②边桩、中柱施作和导洞二衬和③扣拱和拱部土体开挖 3 个典型施工阶段引起的地表沉降比例分别为 6:1:4，与计算得到的比例 5.5:1.5:4.2 略有不同，但比较接近。可以看出，地表最大沉降监测点计算值虽然数值上大于实测值，但各典型施工阶段分担比例与实测结果非常接近，验证了模型与参数的正确性。

      选取模型纵向 10 m 处的管顶节点作为监测点，并与管线 JS14-3 测点的监测结果进行对比分析。管道最终沉降为 60 mm，导洞开挖支护所引起的地表沉降达到了最终沉降的 80.2%左右，施作边桩、中柱以及导洞二衬所引起的地表沉降约占最终沉降的12.5%左右。这两个主要施工阶段总沉降达到最终沉降的 92.7%。后续扣拱、拱部土体开挖，主洞开挖和二衬仅占最终沉降的 7.3%。分析表明，由于管道 JS14-3 测点位于结构南端导洞正上方，受导洞开挖影响比车站结构轴线正上方的地表测点大，故导洞开挖引起的管道沉降所占比例要更大一些。

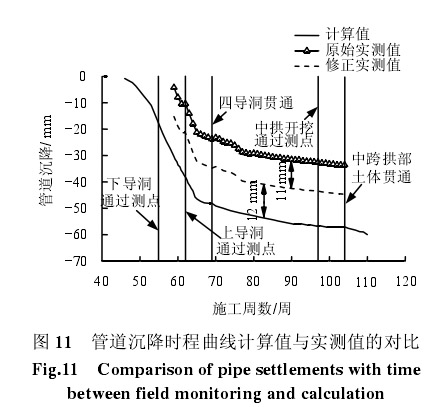
      由于管道初测时，管顶正上方的地表测点已发生部分沉降，其中 JS14-3 测点上方地表沉降为10.2 mm。考虑到地中沉降大于地表沉降，管线未测到的沉降应略大于 10.2 mm，假定未测到的沉降为 11 mm 时，管道沉降实测时程曲线与计算曲线的对比如图 11 所示，虚线为考虑管道未测到的沉降为11 mm 修正后的曲线。实测曲线与计算曲线趋势基本一致，计算值略大于实测值。

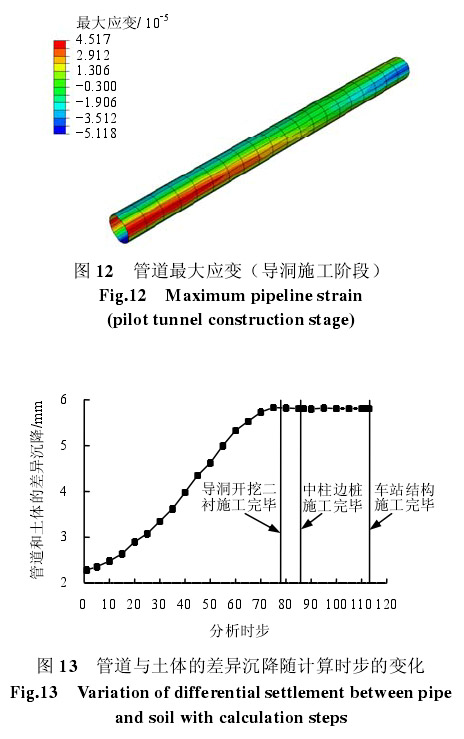
      管线在导洞施工阶段达到最大值，如图 12 所示，可以看出，管道最大应变发生在导洞施工阶段的第 55 个分析步，拉应变为 45 με，压应变为 52 με。导洞施工完毕时拉应变降低为 37 με，压应变为41 με；扣拱、拱部土体开挖完毕时管道拉、压应变稳定在 29 με。

      管道应变在导洞施工阶段达到最大值，导洞施工完毕后逐步下降并最终达到稳定。根据 Attewell等^[8]提出的允许管道应变，最大拉应变 45 με 和压应变 52 με 均小于控制标准，从应变角度可以判断管道在施工过程中是安全的。

      由于管道的刚度远大于土体刚度，管道对地层变形存在一定的抵制作用，造成管道沉降小于周围的土体沉降。管道与土体差异沉降的时程曲线如图13 所示。可以看出，导洞施工阶段管-土差异沉降持续增长，导洞开挖完毕时差异沉降值达到 5.8 mm，随后逐渐趋于稳定。

      （1）洞桩法施工工序复杂、结构力系转换频繁、施工难度大，计算中将施工过程分为 4 个典型阶段：①导洞开挖支护；②施作边桩、中柱以及导洞二衬；③中跨扣拱和拱部土体开挖；④主洞开挖支护及二衬。由于主洞开挖和二衬施工阶段引起的地表沉降很小，故不作统计。数值模拟和现场实测中前 3 个典型施工阶段引起地表沉降的比例分别为 5.5:1.5:4.2 和 6:1:4，二者比较接近。

      （2）刚性接头管道的变形由整个管体共同承担，管道沉降受管道与隧道相对位置关系影响很大，管道正下方土体开挖过程对管道的影响最为显著，由于管道位于导洞上方，故受导洞开挖影响较大，导洞施工阶段发生的沉降量占总沉降的 80.2%。考虑管道未测到的部分沉降后，实测沉降时程曲线与计算曲线吻合较好，各典型施工阶段管道沉降所占比例基本一致。

      （3）管道最大应变发生在导洞施工阶段，受管道正下方土体开挖影响最大，最大拉应变 45 με 和压应变 52 με 均小于控制标准。

      （4）管道与土体的差异沉降主要受管道正下方土体开挖影响，导洞施工阶段管-土差异沉降值持续增长，导洞开挖完毕时管-土差异沉降值达到5.8 mm，掌子面通过后逐渐趋于稳定。

 

[1] 刘维宁, 沈艳峰, 罗富荣. 北京地铁复-八线车站施工对环境影响的预测与分析[J]. 土木工程学报, 2000,33(4): 47－50.

      LIU Wei-ning, SHEN Yan-feng, LUO Fu-rong. Prediction and analysis of effects during construction of subway station (on Fu-Ba line in Beijing) on environment[J].China Civil Engineering Journal, 2000, 33(4): 47－50.

[2] 吴波. 复杂条件下城市地铁隧道施工地表沉降研究[D].成都: 西南交通大学, 2003.

[3] 李大勇. 软土地基深基坑工程邻近地下管线的性状研究[D]. 杭州: 浙江大学, 2001.

[4] 王霆, 刘维宁, 李兴高, 等. 地铁施工影响邻近管线的研究现状与展望[J]. 中国铁道科学, 2006, 27(6): 117－123.

      WANG Ting, LIU Wei-ning, LI Xing-gao, et al. Current situation and prospect of studies on tunneling-induced effect of adjacent pipelines[J]. China Railway Science,2006, 27(6): 117－123.

[5] 何海建. 地铁洞桩法施工对邻近桥桩的影响与控制[D].北京: 北京交通大学, 2007.

[6] 李兴高, 王霆. 柔性管线安全评价的简便方法[J]. 岩土力学, 2008, 29(7): 1861－1864, 1876.

      LI Xing-gao, WANG Ting. Simple method to evaluate the safety of flexible pipelines[J]. Rock and Soil Mechanics,2008, 29(7): 1861－1864, 1876.

[7] 李兴高, 王霆. 刚性管线纵向应变计算及安全评价[J].岩土力学, 2008, 29(12): 3299－3302, 3306.

      LI Xing-gao, WANG Ting. Longitudinal strain calculation and safety evaluation of rigid pipelines[J]. Rock and Soil Mechanics, 2008, 29(12): 3299－3302, 3306.

[8] ATTEWELL P B, YEATES J, SELBY A R. Soil movements induced by tunnelling and their effects on pipelines and structures[M]. London: Blackie and Son Ltd., 1986