摘　要:通过应力控制式循环三轴试验,探讨了地铁行车荷载作用下饱和黄土的累积塑性应变.试验表明:饱和黄土累积塑形应变存在三个典型的发展阶段,即:衰减阶段、稳定阶段和破坏阶段.固结围压、循环试验中的排水条件、动应力及其循环次数、以及动应力比是影响饱和黄土累积塑性应变的重要因素.在排水循环三轴试验中,饱和黄土的累积塑性应变随初始固结围压的增大而减小,随循环次数、动应力和动应力比的增大而增大.基于试验数据,建立了预测饱和黄土累积塑性应变的反正切函数模型.该模型与试验数据符合良好,且仅需三个土体参数,应用比较方便.

关键词:饱和黄土;地铁行车荷载;循环三轴试验;累积塑性应变;动应力比

 

      西安地铁是我国首次在黄土区域建设的地铁线路.地铁建成投入运营后,隧道周围的黄土将不可避免地受到地铁行车荷载的影响.与地震作用相比,地铁行车荷载幅值小,作用时间长,具有间歇性和周期性特征,其长期作用必然对黄土的强度和变形产生较大影响.国内相关研究证实^[1-3],上海地铁建成投入运营后,列车振动引起了明显的隧道轴线沉降,直接威胁到地铁的运行安全,进一步的研究发现,这种影响与地铁运行状态存在很大的相关性.因此,研究地铁行车荷载作用下饱和黄土累积塑性应变的发展规律,对控制列车运行状态、保证西安地铁安全运行具有重要意义.文章通过对不同固结状态下的饱和黄土进行应力控制式循环三轴试验,深入研究了饱和黄土累积塑性应变的发展规律和影响因素,建立了预测饱和黄土累积塑性应变的计算模型,可为估算黄土地区地铁隧道及地表的沉降提供依据.

 

      试验采用电液伺服微机控制动三轴试验机.试验过程中,由微机控制并同步记录施加在试样上的轴向荷载和围压,同时记录试样的轴向变形和孔压.

      试验选取西安有代表性的黏质黄土,取土深度7~8 m,为第四系全新统冲积层.所取土样呈褐黄色,土质均匀,结构较紧密,孔隙发育,含白色钙质结膜和钙质结核,偶见蜗牛壳,可塑,不具湿陷性.其主要物理力学指标为:含水量w=18.4%,湿密度ρ_c=1.594 g/cm³,干密度ρ_d=1.346 g/cm³,液限wL=31.1%,塑限w_P=24.1%,塑限指数I_P=7.0,饱和度S_r=48.86%,孔隙比e=1.028,压缩模量E_1-2=13.7 MPa.

      将所取原状土制备成直径3.91 cm,高8 cm的原状样.用抽真空饱和法对试样进行饱和,经检验饱和度达90%以上.取固结围压分别为50 kPa、100 kPa和150 kPa,固结比为K_c=1.69,将饱和后的试样在不同围压下排水固结,然后施加幅值为±σ_d/2的连续正弦荷载进行循环三轴试验.试验中,参照张曦、唐益群等^[1,4]的研究成果,选用频率为f=2 Hz、σ_d分别为10 kPa、20 kPa、30 kPa和40 kPa的正弦荷载,模拟地铁行车荷载.

 

      间歇性地铁行车荷载作用下,粘性土体经历一个部分排水的变化过程,其超静孔隙水压力能够逐渐消散^[5-6].为了研究不同排水条件下饱和黄土累积塑性应变的发展规律,在固结围压100 kPa,K_c=1.69的状态下,进行不同排水条件的循环三轴试验.

      根据试验数据作出饱和黄土累积塑性应变ε_p与循环次数N的关系曲线(图1).其中,累积塑性应变ε_p是指动应力卸除后土体的残余应变.循环三轴试验中,累积塑性应变在数值上可取σ_d=0时试样的应变值,其与真实值之间的相对误差一般小于10%^[7].

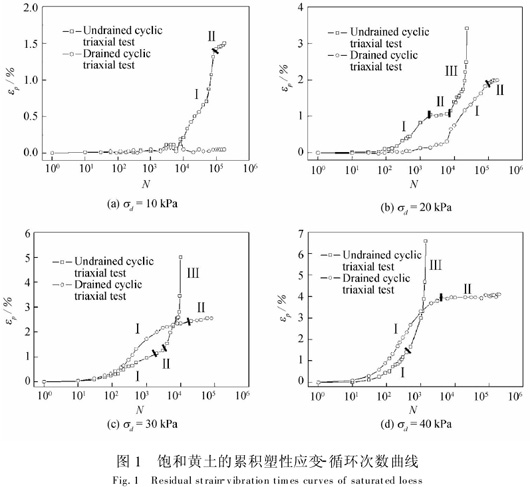
      根据饱和黄土的累积塑性应变与循环次数曲线(图1)可知,饱和黄土累积塑性应变的变化过程存在三个典型的发展阶段.第一阶段( iv):衰减阶段,随循环次数的增大,试样在每个循环内产生的塑性应变逐渐减小;第二阶段( ):稳定阶段,试样在每个循环内不产生或仅产生很小的塑性应变;第三阶段( ):破坏阶段,随循环次数的增大,试样在每个循环内产生的塑性应变逐渐增大,直至试样破坏.

      虽然可将黄土的累积塑形应变划分为衰减、稳定和破坏三个发展阶段,但不是每个试样都表现出完整的三个阶段.这与试样的排水条件和所受动应力大小有关.

      在不排水循环三轴试验中,当动应力为10 kPa时,试样的累积塑性应变在动应力循环作用8 000~90 000次内逐渐增大(图1a);在90 000~175 000次内,试样的累积塑性应变增大很慢,表明试样处于稳定阶段.当动应力为20 kPa、30 kPa时,试样经历衰减阶段并进入稳定阶段后,在动应力达到某一循环次数时,试样的累积塑性应变迅速增大,表明试样进入破坏阶段.同时,动应力越大,试样的稳定阶段越短.动应力为20 kPa时,试样在动应力循环作用2 000~8 000次内处于稳定阶段(图1b);动应力为30 kPa时,试样仅在动应力循环作用2 000~3 000次内处于短暂的稳定阶段(图1c).当动应力为40kPa时,试样的累积塑形应变随着循环次数的增加迅速增大,直至试样破坏(图1d).试样没有出现衰减和稳定阶段.

      在排水循环三轴试验中,当动应力为10 kPa时,试样的累积塑性应变没有随循环次数的增大而明显发展(图1a).当动应力为20 kPa、30 kPa和40 kPa时,试样累积塑形应变的均仅出现了两个发展阶段,即:衰减阶段和稳定阶段(图1b、c和d).即使试样的累积塑形应变已达到4.11%,试样依然出现了稳定阶段(图1d).这与文献[8]中粘土在循环荷载作用下竖向应变随循环次数的变化规律基本一致.

      综上所述,黄土累积塑形应变存在三个典型的发展阶段,即:衰减阶段、稳定阶段和破坏阶段.试样的排水条件不同、所受动应力幅值不同,试样累积塑形应变的发展阶段亦有所不同.

      作出不同排水条件下,循环三轴试验试样的超静孔压Δu与累积塑性应变ε_p的关系曲线(图2).

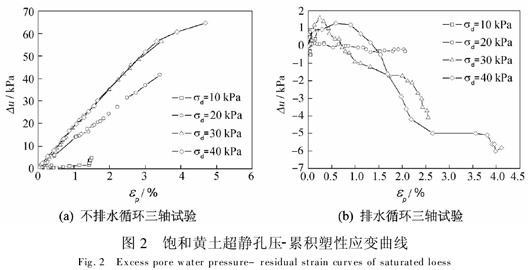
      由超静孔压与累积塑性应变的关系曲线(图2)可知,不同排水条件下的循环三轴试验中,试样超静孔压的变化规律不同.

      不排水循环三轴试验中,除动应力10 kPa外,试样的超静孔压均随累积塑性应变的增大而线性增大.最大超静孔压达到64.7 kPa,约为实测固结围压的60%.

      排水循环三轴试验中,试样均产生了一定的负值超静孔压,且此超静孔压随累积塑性应变的增大而减小.这可能是由于试样在动应力循环作用下出现了不同程度的剪胀引起的.各试样正超静孔压的极值约为1.3 kPa,负超静孔压极值约为-6.0 kPa.

      文献[5]基于现场实测数据报导,地铁振动应力作用下,饱和粘性土体中孔隙水压力的变化幅值不大.在距隧道1.8 m、深度14.0 m处,超静孔压的峰值仅为1.15 kPa.与不同排水条件下,饱和黄土循环三轴试验结果对比可知,不排水条件下,试样内的超静孔压远大于实测值;排水条件下,试样的正超静孔压与实测值比较接近.虽然试样内产生了一定的负超静孔压,但量值不大.

      由此可见,采用排水循环三轴试验研究地铁行车荷载作用下饱和黄土的累积塑性应变是比较合理的.

      一般情况下,土在承受逐级增大的动应力时,可分为振动压密、振动剪切和振动破坏三个反应阶段,以临界强度和极限强度作为三阶段的划分点^[9].

      而本试验中,饱和黄土在小幅值动应力的长期循环作用下,出现了一个延续时间不等的稳定阶段.在此阶段,试样在每个循环内产生的塑性应变极小.

      胡伟^[10]在结构性饱和黄土动力特性研究中亦发现,存在一个塑性残余变形发展缓慢的稳定阶段.在此阶段, 土体初始结构已被破坏,并形成一种更加稳定的土体结构,因而能在一定变形范围内抵抗动应力的循环剪切作用.

      但与文献[10]相比,本文采用的动应力较小,对土体初始结构的破坏作用也较小.动应力促使土粒发生聚合、分裂与转动^[11-12]可能是黄土在小幅值动应力作用下产生累积塑性应变的内在原因.当试样的微结构调整逐渐完成,试样就能适应外部施加的动应力而处于一种平衡状态,其累积塑性应变也不再增大,表现为稳定阶段.如果动应力作用下土粒的分裂作用较强,那么试样的微结构将被逐渐破坏,试样的平衡状态也将被打破,累积塑性应变加快发展,试样由稳定阶段过渡到破坏阶段.

      除循环次数和排水条件外,可能对饱和黄土的累积塑性应变产生重要影响的因素还有:动应力、固结围压和动应力比.对不同固结围压、不同动应力的排水循环三轴试验数据进行整理,以分析各因素之影响.

      整理不同固结围压下排水循环三轴试验数据,得到试样中的ε_p-N曲线(图3).试验发现,以围压50kPa固结的试样只能承受10 kPa和20 kPa的动应力.

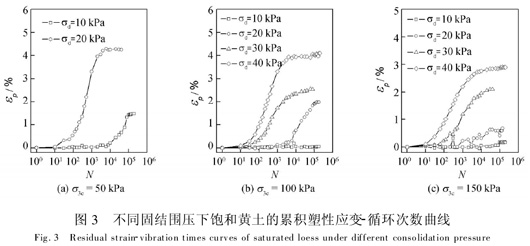
      由饱和黄土累积塑性应变-循环次数曲线(图3)可以看出,不同固结围压下,试样的累积塑性应变都存在比较明显的衰减阶段和稳定阶段.在固结围压相同时,饱和黄土在稳定阶段的累积塑性应变,随着动应力的增大而增大.以固结围压100 kPa为例.动应力10 kPa、20 kPa、30 kPa和40 kPa作用下,试样达到稳定阶段的累积塑性应变依次为0.05%、1.99%、2.55%和4.11%.

      取动应力循环作用至10 000次时,各试样的累积塑性应变进行研究.此时,试样均处于稳定阶段.作出各试样的累积塑性应变随固结围压的变化曲线(图4).

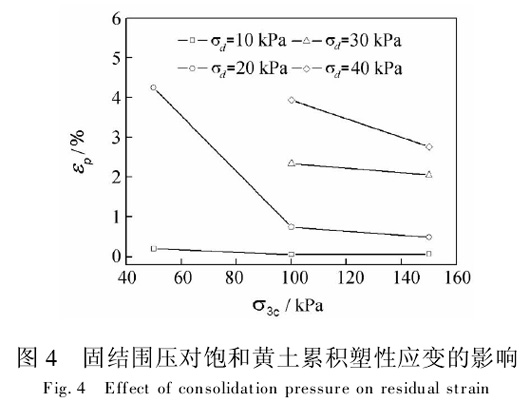
      由固结围压对饱和黄土累积塑性应变的影响(图4)可知,相同动应力作用下,饱和黄土的累积塑性应变随固结围压的增大而减小.以动应力20 kPa循环作用10 000次为例,固结围压为50 kPa、100 kPa和150 kPa的试样,其累积塑性应变分别为4.25%、0.75%和0.49%.

      根据2.2.1节和2.2.2节的分析可知,饱和黄土的累积塑性应变,随动应力的增大而增大,随固结围压的增大而减小.因此,基于这两种影响因素,定义动应力比:

R=σ_d/2σ′₀             (1)

      式中:σ′₀为振前试样的有效固结围压,σ′₀=σ_3c-u₀;σ_3c为试样的固结围压;u₀为试样的超静孔压.

      计算各试样的动应力比,并整理各试样达到稳定阶段时的累积塑性应变εps,得到动应力比对饱和黄土累积塑性应变的影响(图5).

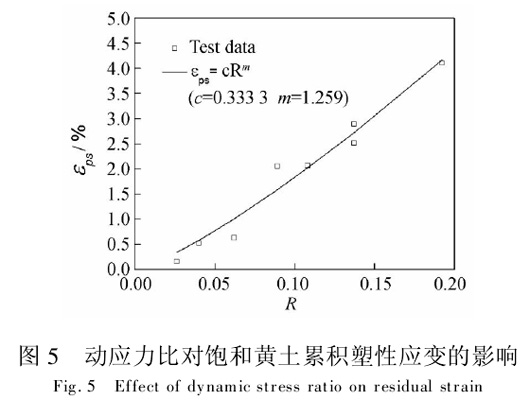
      由动应力比对饱和黄土累积塑性应变的影响(图5)可知,饱和黄土稳定阶段的的累积塑性应变,随动应力比的增大而增大.

      对ε_ps与R之间的关系采用以动应力比为底的指数函数进行拟合,即

ε_ps=cR^m                       (2)

      式中:c、m为反映饱和黄土稳定阶段累积塑性应变与动应力比关系的试验常数.

对本试验,c=3.333×10^-1,m=1.259.拟合结果与试验数据之间的相关系数之平方为0.964,说明公式可以很好地反映动应力比对饱和黄土稳定阶段累积塑性应变的影响.

      通过上述影响因素分析可知:动应力、固结围压和动应力比都是影响饱和黄土累积塑性应变的重要因素.饱和黄土的累积塑性应变随动应力和动应力比的增大而增大,随固结围压的增大而减小.同时,饱和黄土稳定阶段的累积塑性应变与动应力比表现出一定的函数关系.

      为了研究不同动应力比下,饱和黄土累积塑性应变随循环次数的变化规律,采用ε_p/ε_ps对饱和黄土的累积塑性应变进行归一化处理,得到ε_p/ε_ps与循环次数N之间的关系(图6).

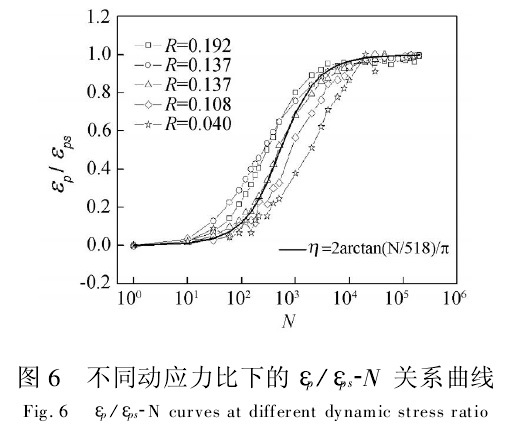
      由ε_p/ε_ps-N曲线(图6)可知,在单对数坐标系中,不同动应力比R下,饱和黄土的ε_p/ε_ps随循环次数N的变化规律都比较接近.同时,ε_p/ε_ps-N曲线形态与反正切函数十分相似,因此采用反正切函数来描述ε_p/ε_ps与N之间的关系,即

η=ε_p/ε_ps=2arctan(N/N_o)/π              (3)

      式中:η为表征饱和黄土累积塑性应变发展规律的参数;N_o为试验常数,反映了饱和黄土的稳定特征,其值为饱和黄土达到稳定阶段所需循环次数的0.5倍.通过对试验数据进行拟合,得N_o=518.拟合数据与试验结果之间的相关系数之平方为0.940,说明式(3)与试验规律符合良好.

      由式(3)得:

ε_p=ηε_ps=2cR^marctan(N/N_o)/π            (4)

      这就是饱和黄土累积塑性应变的反正切函数模型.该模型中包含三个参数c、m和N_o.

      Li和Selig考虑土的动偏应力和静偏应力的影响,修正了Monismith简单指数模型中的参数,得到累积塑性应变模型为^[13]:

ε_p=aβ^mN^b                             (5)

      式中:β为土样承受的动偏应力与静破坏偏应力的比值,β=q_d/q_s;a、m、b为土体参数,取值参见文献[14].

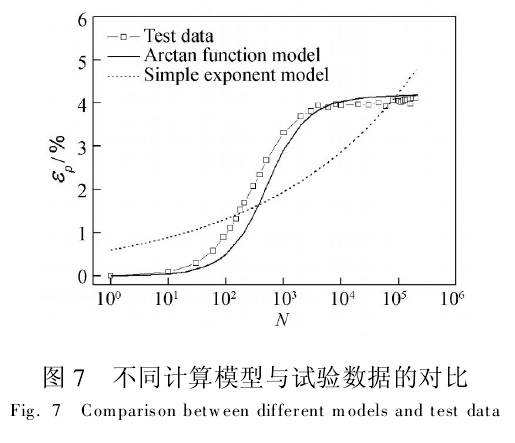
      采用式(4)和(5)计算本次试验中β=0.57,R=0.192的一个试样,并将不同模型的计算结果与试验数据进行对比(图7).其中,应用Monismith简单指数模型进行计算时,取a=1.94、m=2.07、b=0·17.

      通过不同模型与试验数据间的对比(图7)可知:在半对数坐标系ε_p-lgN中,简单指数模型是一个随循环次数单调递增的函数.特别是当循环次数较大(大于80 000次)时,简单指数模型的计算结果迅速增大,导致其与试验数据差异很大,因而不能反映饱和黄土累积塑性应变的稳定阶段.而本文建立的反正切函数模型与试验数据吻合较好,能够比较精确地描述饱和黄土残余应变的发展过程.同时,反正切函数模型仅需三个土体参数即可确定,应用比较方便.

      (1)小幅值地铁行车荷载长期循环作用下,黄土累积塑形应变存在三个典型的发展阶段,即:衰减阶段、稳定阶段和破坏阶段.试样的排水条件不同、所受动应力幅值不同,试样累积塑形应变的发展阶段亦不同.

      (2)不排水循环三轴试验中,试样都产生了较大的超静孔压,且此超静孔压随累积塑性应变的增大而线性增大.排水循环三轴试验中,试样均产生了较小的负值超静孔压.这可能是饱和黄土在循环动应力作用下出现剪胀引起的.与相关实测数据对比发现,采用排水循环三轴试验来研究饱和黄土的累积塑性应变是比较合理的.

      (3)动应力、固结围压和动应力比都是影响饱和黄土累积塑性应变的重要因素.饱和黄土的累积塑

性应变随动应力和动应力比的增大而增大,随固结围压的增大而减小.同时,饱和黄土稳定阶段的累积塑性应变与动应力比表现出一定的函数关系.

      (4)基于反正切函数建立的计算模型,能够反映饱和黄土累积塑性应变的稳定阶段,与相应动应力比下的试验数据吻合较好.该反正切函数模型仅需三个土体参数即可确定,应用比较方便.