地铁隧道中间风井处车箱内瞬变压力分析
摘 要:本文采用动网格技术及三维数值模拟方法模拟地铁列车通过中间风井处的车隧压力波动问题,分析了不同行车速度、不同密封性能条件下车内瞬变压力的变化规律,得出了在列车通过中间风井处是否采用土建工程措施以减低车内瞬变压力而达到人员舒适性的条件。本文研究成果可为城市地铁隧道环控系统设计提供参考。
关键词:地铁隧道 动网格技术 数值模拟 瞬变压力 列车密封性 人员舒适性
0引言
随着轨道交通业的迅猛发展,线路的特征和运行模式也日益呈现多元化,在较长隧道区间由于防灾要求会设置中间风井。当列车通过风井处时,由于隧道断面突变会引起隧道内瞬时压力的变化。根据车辆本身的密封性不同,车体外压力会传递到车内,从而对乘客的舒适性产生影响。与国内外大量专门针对高速铁路列车气动效应的研究不同[1~4],本文重点研究不同车速、不同密封条件下,地铁列车通过中间风井时的瞬变压力波动问题。
由于目前国内尚无地铁压力舒适性标准,本文借鉴美国运输部制定的地铁压力舒适度标准[5],用以判别列车通过中间风井处是否需要采用相应的土建工程措施。该标准要求:①瞬变压力最大值 <700Pa/1.7s;②压力梯度的最大值为 410Pa/s(压力变化时间长于1.7s)。
1 数值计算方法
本文采用三维计算模型模拟地铁列车通过中间风井时引起的空气动力学效应问题,借助CFD模拟软件,并针对隧道空气动力学问题,进行了二次开发,可对车-隧耦合作用的等熵、可压缩粘性气体进行三维分析。为了保证车-隧耦合气动效应计算精度,采用粘性流体假设进行计算,并将空气视为理想气体。模拟采用的数学模型通用表达式如下[6]:
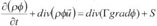
(1)
式中:ρ为密度,φ为通用变量,Г为广义扩散系数,S为源项,
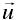
为速度。
由于需要考虑列车在隧道中的运动,在该研究中采用动网格技术模拟列车与隧道间的相对运动[7]。在模拟中采用标准的 k-ε 模型,考虑质量守恒,动量守恒,湍动能守恒及耗散比率守恒。采用耦合式求解器隐式方案对模型进行求解,计算常数C1ε,C2ε,Cμ分别取 1.44,1.92,0.09,Prandtl 数σk和 σε分别取 1.0,1.3。
2 计算条件
2.1 边界条件
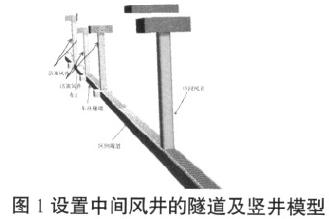
地铁标准车站长度、宽度、高度分别为 120m、4m、4.8m,活塞风井位于盾构井处,其尺寸为:4m×4m×40m(长)。区间隧道长为 2000m,宽为 5.5m,高为 4.8m。车辆长度按 6 节编组考虑为 120m,宽度为 2.8m,车辆高度(车顶距轨面)为 3.8m,阻塞比为 0.40。中间风井的尺寸为:4m×4m×40m(长),模型如图 1 所示。计算中分别考虑了 60km/h、80km/h 和 100km/h 三种行车速度。边界条件设置如下:隧道壁面、地面及列车壁面为考虑粗糙度的墙面边界,滑移体及隧道内部域交界面为投射边界。
2.2车体密封性能
列车的密封情况决定了车外压力传递到车内时,传输的快慢以及车厢内压力的大小。当车辆完全不密封,即车内外空气质量交换完全无阻尼时,车外压力与车内压力相等。当车辆完全密封,即车内外空气无质量交换、车体的刚度又较大时,则车外压力变化对内无影响。在实际中,车辆一般都有一定的密封性,并随着时间的延续,车内外压力逐渐达到平衡,这个延续时间的长短则与车辆的密封特性有关。
采取基于线性假定的泄露模型求解车内压力,即假定车内压力的变化率与车内外压差成正比,如式(2)所示。
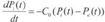
(2)
式中:Pi为车内压力;Pe为车外压力;C0为与车辆密封性有关的常数。
假定 Pe为常数,以 t=0 时 Pi=0 作为边值条件,对式(2)积分得:
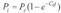
(3)
由于(3)可知,根据该模型,如果将车厢内部抽成真空(即车厢内初始压力为零),则车内的气压将呈指数规律逐渐上升最终同车外压力相等。令
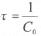
,则 τ为一个具有时间量纲的常数,称为“密封指数”。
对式(2)进行积分时以 t = 0 时,作为边值条件,则得
式中:t 为车内压力泄露的时间;(Pi- Pe)0为初始车内外压差;(Pi- Pe)f为泄露后车内外压差。
由于(5)可知,根据试验测试数据,可以分析计算车体的密封指数。
始值的 38%所需要的泄露时间。铁道部 2001 年《200km/h 及以上速度级列车密封设计级试验鉴定暂行规定》将车内压力从3600Pa降低到1350Pa所需泄露时间定义为密封指数。实际上,两种定义实质是一致的。
指数的调研分析,低密封列车的密封指数范围为:1s<τ<6s。为安全起见,取密封指数的下限值,即取τ=1s,同时与不密封车辆(取 τ=0)进行对比。
3计算结果
以列车60km/h 速度为例,当列车通过中间风井处时,压力分布如图2 所示,车头部压力最高,车尾部压力最低,其他各处的压力介于两者之间。
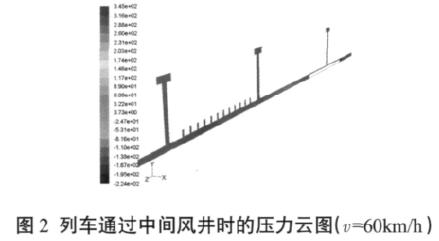
对于非密封性车辆,车体内外压力相同,其波动曲线如图 3 所示,低密封条件下车内压力波动曲线如图 4 所示。计算结果表明,提高车辆密封指数对降低车内压力波动效果明显。
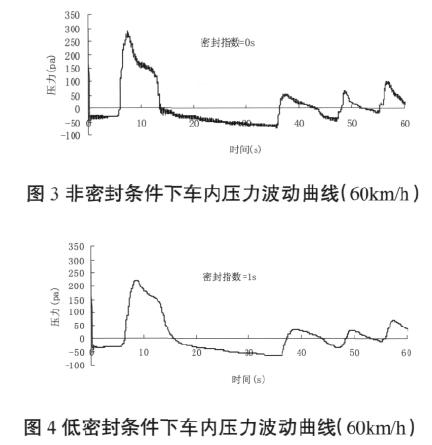
不同车速、不同密封条件下,列车通过中间风井处车厢瞬变压力的计算结果如表 1 所示,车厢内瞬变压力随行车速度的增加而增加。依据选定的压力舒适度标准,在非密封列车情况下,在行车速度≤80km/h时,瞬变压力可满足标准要求;在行车速度≥100km/h时,中间风井处需设置渐变扩大措施以确保压力突变在标准允许范围内。在低密封列车情况下(τ=1s),当行车速度≤100km/h 时,瞬变压力可满足标准要求。

4 结论
本文利用动网格技术采用三维数值模拟方法模拟了地铁列车通过中间风井处的车隧压力波动问题,可以得出以下结论:
1)车密封指数对车厢内瞬变压力影响明显;
2)车厢内瞬变压力随行车速度的增加而增加;
3)于低密封地铁列车,当列车以小于100km/h的时速经过中间风井时,车内压力波动满足人体舒适标准要求,无需设置土建缓冲措施;对于非密封车辆,列车以 100km/h 的时速通过中间风井时,需要采用渐变的土建工程措施才能满足人员舒适性要求。
参考文献
[1]骆建军,王梦恕,高波,等.高速列车进入带缓冲结构隧道的压力变化研究[J].空气动力学学报, 2007, 25(4): 488-494
[2]王建宇,万晓燕,吴剑.高速铁路隧道瞬变气压和乘车舒适度准则[J].现代隧道技术, 2008, (2): 25-28
[3] K Kikuchi, S Ozawa, H Takami, et al. Continuous pressure waves enerated by a train running in a tunnel [J]. Journal of Low requency Noise Vibration and Active Control, 2009, 28 (2):117-132
[4]韩华轩,王英学.客运专线山区长隧道的乘客气压舒适度研究[J].石家庄铁道学院学报(自然科学版), 2009, 22(2): 68-72
[5]温竹茵,周质炎.高速列车隧道的空气动力学效应及解决措施[R].上海:上海国际隧道工程研讨会, 2003
[6]周光垌,严宗毅,许世雄,等.流体力学[M].北京:高等教育出版社, 2000