扁铲侧胀消散试验求解固结系数的研究
提 要 通过对扁铲侧胀消散试验的机理进行分析,推导出扁铲侧胀消散试验中所测得的压力值与孔隙水压力之间的关系,进而提出根据扁铲侧胀消散试验资料绘制超孔隙水压力消散曲线的方法。采用计算机数值模拟的方法,得到扁铲探头贯入后,周围土体中超孔隙水压力在空间的分布规律,并将其作为求解固结微分方程的初始条件。通过对固结微分方程的求解,导出利用扁铲侧胀消散试验中超孔隙水压力随时间的变化及在空间的分布规律,提出用扁铲侧胀消散试验资料估算土体水平固结系数的方法。结合杭州地铁一号线工程勘察中二个工程所做的扁铲侧胀消散试验的实测数据资料,对本文的估算方法进行了验证。与室内土工试验的成果进行对比,结果令人满意。
关键词 固结系数 扁铲侧胀消散试验 固结微分方程
1 引言
固结系数Ck是软土地基变形分析与设计计算的关键参数,长期以来Ck主要是通过室内土工试验来测定的。但是在软土地区,取土会对原位土体造成较大的扰动,要取得高质量的土样比较困难,所以用室内土工试验的方法来测定Ck,难以取得令人满意的结果,对于结构性比较强的细粒土,室内测定的固结系数可能比现场值低一到二个数量级。通过简单的原位试验获取土体固结系数成为岩土工程界努力的方向。
扁铲侧胀试验(DMT)是Marchtti发明的、国内也在开发应用的一种原位测试手段[1~3]。扁平状测头压入时对土体的扰动性较小,能更加真实地反映原位土体的性质,所以应用扁铲侧胀消散试验来求解土体固结系数,对于工程实践具有积极的意义。
2 消散试验中的超孔隙水压力
2.1 扁铲侧胀消散试验中的超孔隙水压力
扁铲测头贯入时,周围土体中产生了超孔隙水压力,达到试验深度后,开始进行消散试验。设膜片位于基座处时土体的水平总应力为σhJ,孔隙水压力为u,土体的有效应力为σ′hJ,根据有效应力原理有:
σhJ=u+σ′hJ (1)
式中,σhJ即为P0,P0是测头膜片处于基座时测得的压力值.
土体的有效应力σ′hJ可以表示为:
σ′hJ=σ′h0+Δσ′h0 (2)
由式(1)和式(2)得:
u=P0-σ′h0-Δσ′h0 (3)
式中,σ′h0为原位土体的水平有效应力;Δσ′h0为扁铲测头贯入土体后所引起的土体水平方向的附加有效应力。
σ′h0=K0σ′v0 (4)
式中,σ′v0为原位土体的竖向有效应力,K0为土体的静止侧压力系数。
2.2 超孔隙水压力的表达式
根据唐世栋等的研究[4]
Δσ′h0= 0.30ΔP= 0.30(P1-P0) (5)
式中,P1为测头膜片离基座1.10mm时测得的压力值。
综合式(3)、(4)、(5)得
u= 1.3P0-0.3P1-K0σ′v0 (6)
扁铲测头的压力值P0,P1为:
P0= 1.05(A+ΔA)-0.05(B-ΔB) (7)
P1=B-ΔB (8)
式中,A、B为试验实测值,ΔA、ΔB为膜片标定值。
根据唐世栋、肖勇对杭州地区的研究[5]:
K0=nKD (9)
式中,系数n由土层的材料指数ID值来确定:当ID≤0.6时,n=0.085;当0.6<ID<3.3时,n=0.2;KD为水平应力指数。
KD= (P0-U0)/σ′v0 (10)
综合式(6)、(7)、(8)、(9)、(10)得:
u=(1.3-n)P0-0.3P1+nU0= (1.365-1.05n)(A+ΔA)- (0.365-0.05n)(B-ΔB)+nU0 (11)
式中,U0为静水压力值。
式(11)即为扁铲侧胀消散(DMT-A2)试验中的孔隙水压力表达式。但是式(11)只适用于求解u1(即第一次测读A、B值所对应的孔隙水压力)。为了得到任意时刻的孔隙水压力,本文考虑引入一个孔隙水压力u和A+ΔA值的比例系数β,定义为:
β=u1/(A1+ΔA) = [(1.365-1.05n)(A1+ΔA)- (0.365-0.05n)(B1-ΔB)+ nU0]/(A1+ΔA) (12)
考虑到试验时对A、B值的测读习惯,并为了简化计算,假设在任意时刻测读Ai值时,孔隙水压力ui和Ai+ΔA的比值保持不变,那么任意时刻的孔隙水压力ui可以用下式来估算:
ui=β(Ai+ΔA) (13)
通过试验中对Ai值的测定,可以根据式(13)得到超孔隙水压力随时间消散的曲线。
3 求解固结方程及估算水平固结系数
3.1 扁铲贯入产生的初始超孔隙水压力
超孔隙水压力在空间的分布是求解土体固结系数的初始条件。本文尝试利用数值分析程序ANSYS对扁铲测头的贯入过程进行模拟,从而得出测头贯入后周围土体中超孔隙水压力分布的模拟数值解。数值模拟的结果表明,虽然扁铲测头和圆锥探头在边界条件上有所不同,但超孔隙水压力在空间的初始分布规律在形式上仍然符合应变路径法的负指数分布规律,即:
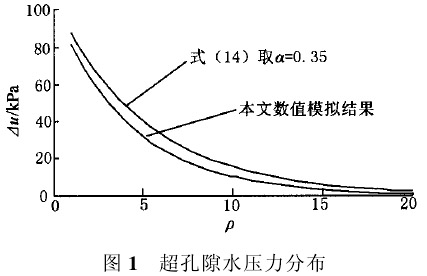
u(ρ)=ume-α(ρ-1) (14)
式中,um为扁铲测头表面膜片处的超孔隙水压力;ρ=r/S,r为扁铲测头膜片一侧的土体中一点到测头中心线的距离,S为扁铲测头厚度的一半,即7.5mm;α为一正值,根据以往研究的结果[6],其范围在0.15~0.40之间。
按式(14)和本文数值模拟得到的超孔隙水压力随距离的变化对比曲线如图1所示。根据数值模拟的结果[7],扁铲测头贯入后一侧明显受压缩的土层厚度H大约为4S,如图2所示。

3.2 固结微分方程
太沙基单向固结的基本微分方程:
令ρ=r/S,并加入时间因数T=Cht/H2(H为扁铲探头膜片一侧受压缩土层的厚度),则式(15)可以表示为:
式(16)为探头膜片附近超孔隙水压力消散的固结微分方程,求其满足式(14)的解,就能得到土体中超孔隙水压力um随着距离和时间的变化关系式。
3.3 求解固结微分方程
上面的问题归结为求解下列数学问题(为使式子简化,常数H2/S2记为D):
至于另外的一些条件,如T=∞时,u=0;ρ=∞时,u=0能自动满足,求解时可以不予特别考虑。
用分离变量法,设
u(ρ,T)=R(ρ)Γ(T) (19)
是式(17)的一个解。那么将式(19)代入到式(17)后,可得到两个常微分方程。它们的解为:
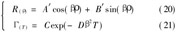
将式(20)、(21)代入式(19),可以得到式(17)的一个解:
式中,β为正实常数;A=A′C、B=B′C也都为任意实常数。
因为对于任意正实数β,式(22)都能够满足式(17),所以可以写出一个无穷多解的连续集合如下:
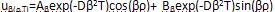 (23)
(23)
在式中,对于每一个β值,A和B也可有不同的对应值,即A和B都是β的函数。由于式(23)对于任一β值总是能满足式(17),因此无穷多个函数uβ的线性组合:
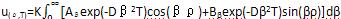 (24)
(24)
也必定满足式(17)。此处K为一任意常数。令K=1/π,则有:
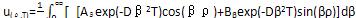
(25)
为满足任意初始条件u(ρ,0)=f(ρ),应有:
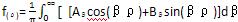
(26)
式(26)表示未知函数Aβ和Bβ就是fρ的余弦和正弦变换,即:
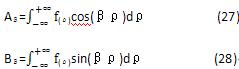
将式(27)、(28)所示的余弦和正弦变换代回式(25),可以得:
在以上的变换过程中,为了避免混淆,已经将余弦和正弦变换中的变量ρ换成了x。
注意到三角恒等式
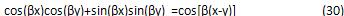
则式(29)可化为:
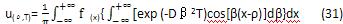
式(31)花括号内的积分式可以容易的解出:
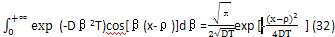
将式(32)代入式(31),则有:
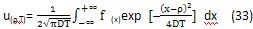
由于式(18)是定义在上[1,+∞)的初始条件,所以为了求解式(33)中(-∞,+∞)范围内的积分,可以按照解析开拓原理将式(18)所确定的函数解析开拓到整个(-∞,+∞)区域内,即:
u(ρ,T=0)=ume-α(|ρ|-1) (34)
将式(34)代入式(33),得:
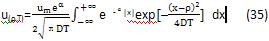
那么问题转化为求解积分式:
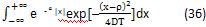
将此定积分拆成在(-∞,0)和(0,+∞)区域上和的形式,并分别记为F1和F2,如下式所示:
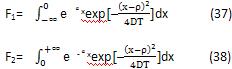
利用用分部积分法,可以容易地解出积分式F1和F2,如下式所示:
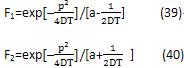
再结合式(35)、(39)、(40),便可以得到:
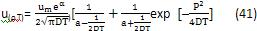
式(41)是所求固结问题的最后解,它是扁铲探头贯入后,超孔隙水压力随时间的变化以及在空间的分布规律。
3.4 水平固结系数的估算
用扁铲侧胀消散试验所得到的超孔隙水压力消散资料,相当于ρ=1处的超孔隙水压力的消散资料。将ρ=1代入式(41)中,并取H=4S,即D=16,可得扁铲测头处土体中超孔隙水压力消散与时间因数T之间的关系式:
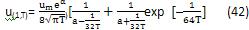
图3的理论曲线是按式(42)取α=0.4绘出的。表1给出了按此计算的部分结果。由图3或表1可以求得超孔隙水压力消散到某一程度所对应的时间因数T值,利用扁铲侧胀消散试验可以求得到达该固结度所需要的时间t,这样,土体的水平固结系数Ch可以用下式来估算:

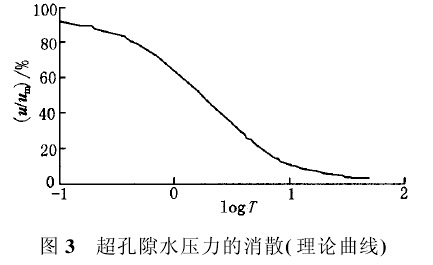
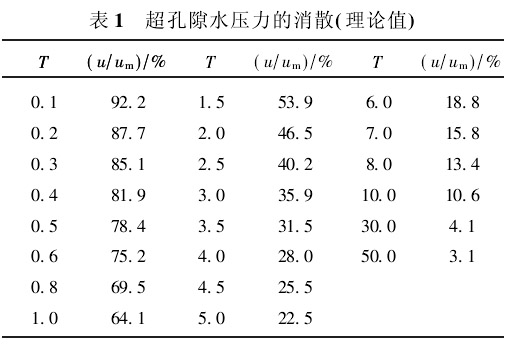
在利用式(43)来估算土体的水平固结系数时,还存在着选用哪一个固结度作为计算点的问题。表2列出了α分别取0.15和0.4时用式(42)进行计算的结果。从该表中可以看出,超孔隙水压力的初始分布对计算结果有一定的影响。这种影响随着固结时间的增加(即u/um值的减小)越来越明显。所以不能以太大的固结度作为计算点。

但是另一方面,扁铲测头停止贯入后周围土体的应力松弛对固结初期的超孔隙水压力的消散有一定的影响,因而作为计算点的固结时间也不宜过短。本文考虑将固结度达到50%时所对应的时间作为估算固结系数的计算点。同样的实测资料也与α=0.15时的理论曲线进行了对比,离散性明显增加。由此可知,α取高值时理论曲线与实测结果更为吻合。当α=0.4时,按照表2计算的结果,当固结度达到50%时,时间因数T=1.469,将其代入式(43)可以得到:
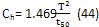
式(44)即为根据扁铲侧胀试验实测资料估算土体水平固结系数的计算公式。
杭州4 工程实例的验证
地铁一号线工程(临平—萧山)的勘察中,进行了扁铲侧胀消散试验,共获得了“九堡东站”和“红普路站”6个试验孔24个试验点的DMT-A2消散试验实测资料。现选取4个有代表性的试验点的实测资料做出其超孔隙水压力的消散曲线,如图4所示,可以得到四个试验点的t50分别为69s、50s、273s、415s,代入式(44)就可以估算出四个试验点处土体的水平固结系数。
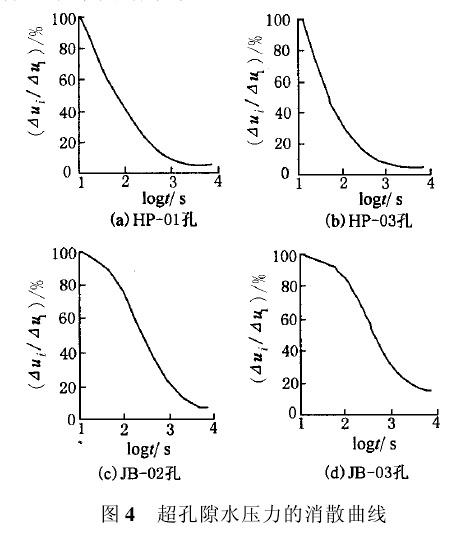
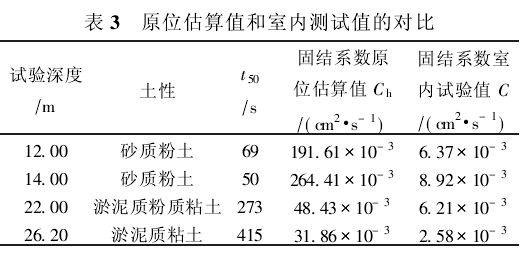
表3出了用式(44)估算的原位水平固结系数,当土性为砂质粉土时,估算值和室内土工试验测得的固结系数相比约大30倍;当土性为淤泥质粉质粘土时,估算值约大8倍;当土性为淤泥质粘土时,估算值约大15倍。参照以往的工程实践资料,室内土工试验所测的土体固结系数往往是偏小的,式(44)的估算值可能更接近于实际值,这还需要更多工程实践来验证。
5 结论
1)铲侧胀消散试验中,通过实测压力值A的变化,可以反映测头附近土体中超孔隙水压力的消散过程。
2)数值模拟方法,可得到扁铲测头贯入土中时的影响及其产生的超孔隙水压力在空间的分布。以此作为初始条件,求解固结微分方程,得出超孔隙水压力在时间和空间的变化规律,如式(42)。
3)固结度为50%时的试验曲线和理论曲线,可估算土体的水平向固结系数。
4)文方法对杭州地铁一号线2个车站的原位水平固结系数进行估算,在不同土性的对比中,试验估算值比室内土工结果要大8~30倍,对比室内土工试验的结果以及以往的工程经验,估算的结果总体上是令人满意的。
5)用扁铲侧胀消散试验求解土体固结系数的方法,是基于理论推导的结果,但在推导过程中也利用了杭州地区的扁铲侧胀试验资料的半理论半经验性公式。本文的方法是否适用于其他地区还需要扁铲侧胀消散试验的推广以及更多的实际工程资料的验证。
参考文献
1 Marchetti S.The flat dilatometer (DMT) and its applications to geotechnical design.Tokyo:Japanese Geotechnical Society International Seminar,1999:56~61
2 陈国民.扁铲侧胀仪试验及其应用.岩土工程学报,1999,21(2):177~183
3 唐世栋,林华国.用扁铲侧胀试验求解侧向基床反力系数.岩土工程学报,2003, 25 (6):692~696
4 唐世栋,吕健春,傅纵.扁铲侧胀试验求解初始水平应力和静止侧压力系数.岩土工程学报,2006,28(12):2144~2148
5 唐世栋,肖勇,王松平.杭州地区用扁铲侧胀试验求解静止侧压力系数K0的研究.工程勘察,2009,(7):5~9
6 朱小林,唐世栋.利用孔隙水压力-静力触探探头估算软粘土固结系数的理论分析.工程勘察,1986,(6):8~12
7 肖勇.扁铲侧胀消散试验求解水平固结系数和渗透系数的研究:[学位论文].上海:同济大学,2009