武汉地区饱和黏性土热物理性质试验研究
摘 要:根据三相土的组成特点,研究饱和黏性土热物理性质与其含水量、密度及孔隙比等参数间的关系。在武汉地铁详勘阶段,采取一级阶地黏性土饱和原状土样, 利用 KD2 Pro Thermal Properties Analyzer 热参数分析仪进行热物理性质试验,同时测试土样的含水量及密度。 对试验结果进行回归分析,分析时假设土中水及固体颗粒骨架的热物理性质为定值,且土中水分没有明显的迁移。结果表明:黏性土导热系数随原状土样密度的增加而增加,随孔隙比的增加而降低;比热容随原状土样含水量的增加而增加。 结合试验结果及国外的经验公式,给出了便于工程使用的导热系数及比热容计算公式。
关键词:三相土;饱和黏性土;热物理性质;含水量;密度;孔隙比
土体是由大小不同、形状各异的固体颗粒和孔隙以一定的形式连接形成的多孔介质。 多孔介质中的热质迁移是多相体系非连续介质的复杂过程。 传热研究的主要内容就是研究传热传质的基本规律以及具体应用,计算给定条件下的传热传质的速率及其控制,寻找传热强化及削弱的技术途径[1]。含湿多孔介质的湿热迁移特性数据包括导热系数、比热容及导温系数等,其大小受密度、含水量及化学成分等因素的影响[1-2]。
导热系数的确定方法,包括实验室[3-4]测试和现场直接测定[5-6];根据测试原理可分为稳态法及瞬态法[7] ;根据热源的几何形状可分为热线法、热条法及面热源法。 稳态法是给试样施加一定的温度梯度,并使其达到稳定传热状态,进而确定介质导热系数。 由于稳态法一般需要较长的试验时间,而且试验过程中土样的水分在总压力梯度、湿度梯度及温度梯度作用下很容易发生迁移,致使含水率不均匀,影响试验结果[1,7],故实验室一般采用瞬态法,目前常用的探针法便属于瞬态法[3,4,7]。
除了直接测定外,采用BP 神经网络[8]及分形模型理论[9]计算导热系数的方法也有报道。通过分析热物理性质与土工参数的关系,进而给出热物理性质的经验计算公式也是当前研究的热点[10-12]。
笔者通过对武汉地区一级阶地黏性土饱和原状土样导热系数、比热容、密度及含水量测试,分析各组分以并联形式对整体热物理性质的影响,并以测试数据的统计结果为基础,提出根据土体含水量计算比热容的经验公式及根据密度、孔隙比(率)计算导热系数的经验公式。
1 武汉地区岩土层分布情况
武汉市地处长江中下游,跨越长江两岸,为长江河谷的一部分,属低丘陵-平原地貌。 武汉市区可分为3 个地貌单元:剥蚀丘陵区、剥蚀堆积垄岗区及河流堆积平原区。
根据武汉地区地铁沿线工程地质勘察成果可知,地铁沿线地层分布情况为:
1)一级阶地全新统冲积及冲洪积成因一般黏性土,软土,砂土及卵、砾石层。 表层一般为可塑黏性土,即硬壳层。
2)二级阶地堆积平原区上更新统冲积及冲湖积成因一般黏性土,软土,砂土及含黏土质卵、砾石层。
3)三级阶地剥蚀堆积垄岗区上更新统-中更新统冲洪积一般黏性土,局部夹碎石层。
4)长江、汉江故河道中更新统-下更新统冲洪积含黏性土砂层及卵、砾石层,局部夹透镜体状黏性土层。
5)残积土层及基岩层。
其中一级阶地黏性土(Q4al+pl)在汉口及武昌沿江地区分布较广泛,呈厚层状分布。 该层黏性土呈灰、褐灰、褐黄色,饱和,切面较光滑,干强度及韧性中等,呈可塑-软塑状态。
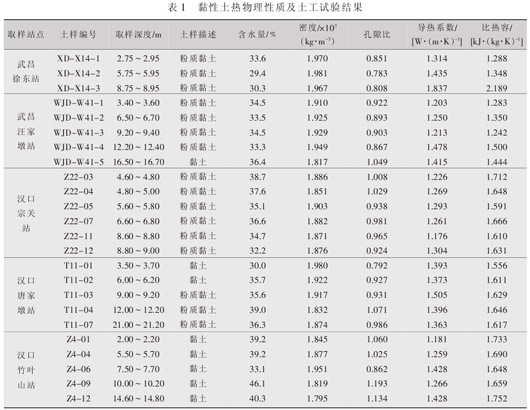
当形成年代及沉积环境相同时,同一土层因化学成分基本相同,其热物理性质与土样密度、土样含水量及其他因素有关。 为保证试验土样的代表性,试验所取24 组原状土样位于地面下 2.00~22.00 m 范围内,分布于长江南岸及北岸的一级阶地的 5 处不同地段,均为饱和黏性土(具体情况见表 1)。
2 热物理性质的试验方法
探针法是测试饱和土导热系数的有效方法之一,它具有制造成本低廉、测定仪器简单、测定时间短和准确度较高等优点。 探针是利用瞬态线热源原理测试导热系数的有效手段,试验时土样基本上保持原有密度及湿度,使测定结果更符合实际情况[7]。
试验中导热系数λ 采用美国 Decagon Devices,Inc.KD2 Pro Thermal Properties Analyzer 热参数分析仪确定。在试验中,控制 Q 为常量,于是线热源处温度 T的测量值与时间lnt 之间便呈直线关系,而被测介质的热导率即由该直线的斜率来确定。
比热容通常在探针法测定导热系数时,通过配置SH-Sensor 双探针测定。
3 试验结果
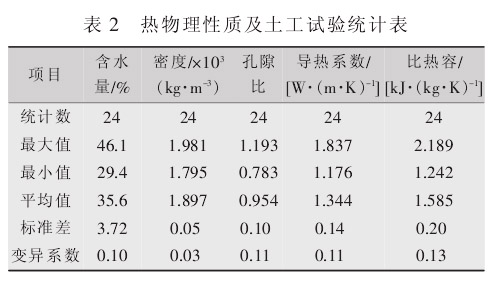
饱和原状土样热物理性质及土工参数试验结果见表1,统计结果见表 2。
4 试验数据分析
4. 1 导热系数分析及评价
4. 1. 1 导热系数计算公式
一般情况下,土是由固、液、气三相组成的。 由于很难对多孔介质的几何参量作严格的描述,所以一般将多孔介质看作在大尺度上假想均匀分布的虚拟连续介质[1]。 根据瞬态线热源的工作原理,试验过程中土样基本上保持原有密度及湿度[7],一般认为水及固体颗粒的导热系数为定值。 根据以上假设,当考虑各组分以并联形式参与对整体的贡献时[13-14],土体的导热系数计算公式(采用体积百分比)为:
λ=(λsvs+λlvl+λgvg)/(vs+vl+vg)。 (1)
式中:λs、λl及λg分别为固体颗粒、颗粒间液体及颗粒间气体的导热系数,W·(m·K)-1; vs、vl及vg分别为固体颗粒、颗粒间液体及颗粒间气体的体积,m3。
试验所取原状土样均饱和,颗粒间气体的体积及导热系数均较小,故一般忽略不计。 令 vs=1.0,ρw= 1.0×103kg·m-3,sr=100 %,则式(1)可简化为
λ=λl+(λs -λl)/(1+e), (2)
也可表示为
λ=λl·ρ/ρw+(λs -λl·ds)/(1+e)。 (3)
式中:e 为土样孔隙比,无量纲;ρ 及 ρw分别为土样及纯水密度,×103kg·m-3;ds为固体颗粒的土粒比重,无量纲。
4. 1. 2 导热系数数学拟合及分析
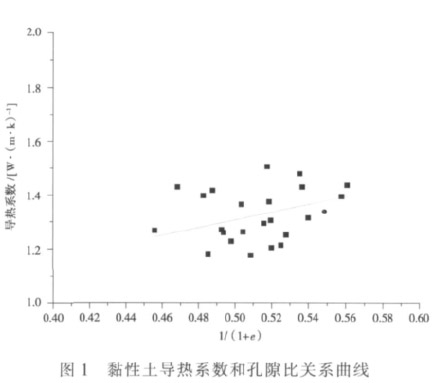
1)由式(2)可知,导热系数λ与 1/(1+e)呈线性关系,故对表 1 中 24 组数据进行线性拟合,显著性水平α=0.05,拟合曲线见图 1,拟合结果为
λ= 0.59+1.43/(1+e)。 (4)
式(4)的残差平方和为 0.203 12,决定系数为 0.994 75,拟合结果显著。
2)当黏性土孔隙比 e 为零时,相当于无孔隙的岩石,此时黏性土的导热系数为固体颗粒的导热系数,由式(4)有λs=2.02 W·(m·K)-1,与页岩的导热系数基本一致;当固体颗粒完全被水代替时,即为纯水,此时导热系数为水的导热系数,由式(4)有
λl = 0.59 W·(m·k)-1。
对一级阶地黏性土,ds=2.71,式(3)可转化为:
λ= 0.59ρ+0.42 /(1+e)。 (5)
式(5)的残差平方和为0.411,决定系数为 0.989 84。拟合效果显著。
4. 1. 3 与 Johnsen 的经验公式对比
Johnsen 对土的导热系数进行了深入研究,归纳出饱和土体导热系数的经验公式[7]为:
λ=λl n·λs(1-n)。 (6)
式中:λl为颗粒间液体导热系数,一般取经验值λl=0.57 W·(m·K)-1;λs为固体颗粒导热系数as=7.7a×2.0(1-a),a为石英含量,由于一级阶地黏性土以黏土矿物为主要成分,a 近似为零,故λs=2.00 W·(m·K)-1。 式(6)经验值与式(4)拟合结果基本一致。
式(6)适用于各种类型砂土及砂土混合物,其导热系数由孔隙率及颗粒的石英含量决定。 当土样中固体颗粒主要由黏土矿物构成时,便不宜直接采用式(6)计算黏性土土样的导热系数。
事实上,根据式(2)的拟合结果,将λl=0.59 W·(m·K)-1、λs=2.02 W·(m·K)-1代入式(6)中,发现其计算值较试验值普遍偏小,误差值约为-15%。根据分析结果,建议按修正后的式(7)来计算黏性土导热系数,即:
λ=λl n·λs(1-n)+0.22。 (7)
式(7)的残差平方和为 0.406,决定系数为 0.98997。拟合效果显著。
4. 2 比热容分析及评价
4. 2. 1 比热容计算公式推导
当固体颗粒、颗粒间液体及颗粒间气体以并联形式参与对整体比热容的贡献时,土体比热容的计算公式(采用质量百分比)为:
c=(cs·ms+cl·ml+cg·mg)/(ms+ml+ mg)。 (8)
式中:cs、cl及cg分别为固体颗粒、颗粒间液体及颗粒间气体的比热容,kJ·(kg·K)-1; ms、ml及mg分别为固体颗粒、颗粒间液体及颗粒间气体的质量,kg。
试验所取原状土样均饱和,由于颗粒间气体的质量及比热容均较小,故一般忽略不计。 令 vs=1.0,ρw=1.0×103kg·m-3,sr=100 %,则式(8)可简化为:
c= cl-(cl-cs)/(1+ w)。 (9)
式中:w 为土样含水量,无量纲。
4. 2. 2 比热容数学拟合及分析
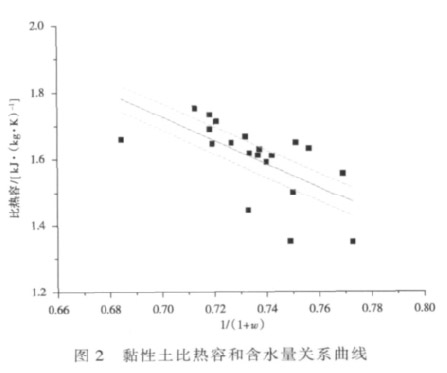
1)由式(9)可知:比热容随含水量的增加而增加,故对表1 中 24 组数据进行线性拟合,显著性水平 α=0.05,拟合曲线见图 2,拟合结果见式(10):
c= 4.20-3.53/(1+w)。 (10)
式(10)的残差平方和为 0.147 91,决定系数为 0.996 86,拟合结果显著。
2)当黏性土含水量 w 为零时,相当于干燥的岩石,此时黏性土的比热容为固体颗粒的比热容,由式(10)有cs=0.67 kJ·(kg·K)-1;当固体颗粒完全被水代替时,即为纯水,此时比热容为水的比热容,由式(10)有cl=4.20 kJ·(kg·K)-1。
3)由于水的比热容大于固体颗粒的比热容,随含水量的增加,饱和土体中液体所占的比例相应增加,导致比热容增加。
5 结论
1)当黏性土孔隙比 e 为零时,相当于无孔隙的岩石,此时黏性土的导热系数为固体颗粒的导热系数,与页岩的导热系数基本一致;当固体颗粒完全被水代替时,即为纯水,此时导热系数为水的导热系数。
2)当黏性土含水量 w 为零时,相当于干燥的岩石,此时黏性土的比热容为固体颗粒的比热容;当固体颗粒完全被水代替时,即为纯水,此时比热容为水的比热容。
3)饱和土体比热容值随含水量增大而增大,含水量和比热容呈非线性关系。对一级阶地黏性土,比热容和含水量经验计算公式可表示为c= 4.20-3.53/(1+ w)。
4)饱和土体导热系数随密度的增加而增加,随孔隙比的增加而降低。 对一级阶地黏性土,导热系数和孔隙比经验计算公式可表示为λ=0.59+1.43/(1+e)。 导热系数和密度及孔隙比经验计算公式可表示为λ=0.59ρ + 0.42/(1+ e)。
文中所得经验公式仅适用于武汉地区一级阶地黏性土,其他地区热物理性质与土工参数间经验关系有待于当地经验关系的积累和整理。
参考文献:
[1] 王补宣. 多孔介质中的对流传热传质[J]. 西安交通大学学报,1994,28(5):51-58.
[2] 首都规划建设委员会办公室. GB 50307-1999 地下铁路 、轻轨交通岩土工程勘察规范[S]. 北京:中国计划出版社,2000.
[3] 张旭,高晓兵. 华东地区土壤及土沙混合物导热系数的实验研究[J]. 暖通空调,2004,34(5):83-86.
[4] 孟凡凤,李香龙,吴晓辉,等. 利用探针法测定土壤的导热系数[J]. 绝缘材料,2006,39(6):65-66,70.
[5] 于明志,方肇洪. 现场测量深层岩土热物性方法[J]. 工程热物理学报,2002,23(3):354-356.
[6] 于明志,方肇洪. 现场测试地下岩土平均热物性参数方法[J].热力动力工程,2002,17(5):489-493.
[7] 陈善雄 ,陈守义. 砂土热导率的实验研究[J]. 岩土工程学报 ,1994,16(5):47-53.
[8] 何发祥,黄英. 用 BP 网络求解土体的导热系数[J]. 岩土力学,2000,21(1):84-87.
[9] 徐琳,张旭,徐进波.土壤样品有效导热系数的分形计算模型[J]. 可再生能源,2009,27(1):81-84,87.
[10] 肖琳 ,李晓昭 ,赵晓豹 ,等. 含水量与孔隙率对土体热导率影响的室内实验[J]. 解放军理工大学学报 : 自然科学版 ,2008,9(3):241-247.
[11] 苏天明 ,刘彤 ,李晓昭 ,等. 南京地区土体热物理性质测试与分析[J]. 岩土力学与工程学报,2006,26(5):1278-1283.
[12] 蒋建平 ,李晓昭 ,高广运 ,等. 南京地铁 (融 )土热物理参数试验研究[J]. 中国铁道科学,2009,30(1):13-16.
[13] 刘为民,何平,张钊. 土体导热系数的评价与计算[J]. 冰川冻土,2002,24(6):770-773.
[14] 沈珍瑶,李国鼎,李书绅. 高压实膨润土的导热性能[J]. 大坝观测与土工测试,1998,22(3):39-40