11号线徐家汇站深基坑降水数值模拟
摘 要:承压水是基坑工程施工主要风险源之一,基坑降水是地铁站建设经常采取的措施。承压水降水设计应综合考虑水位降深要求、承压含水层厚度、降水井深度、止水帷幕深度等因素,通常采用数值模拟方式进行计算分析。本文以上海地铁 11 号线徐家汇站深基坑降水工程为例,根据场地工程地质和水文地质条件、地铁站围护结构设计深度和基坑开挖深度,建立地下水渗流三维数学模型,通过单孔和群孔抽水试验资料反求水文地质参数,结合场地初始条件和边界条件,采用 Visual Modflow 有限差分法对基坑降水进行模拟,数值模拟结果与地下水位实际监测数据十分吻合,为地铁工程深基坑降水设计提供了指导作用。
关键词: 承压水; 降水井; 止水帷幕; 深基坑; Visual Modflow; 数值模拟
1 引 言
地铁站建设因基坑开挖深度较大常常要采取工程降水措施,如何合理地计算地铁站基坑涌水量大小及坑内外水头的分布,对降水方案和围护结构设计进行优化,控制周围地面沉降的发生具有重要意义。目前关于地下水问题的计算,数值模拟仍然是一种行之有效的途径。国内外关于工程降水数值模拟计算的成果较多,其中对场地地质条件的深入研究是准确建立数学模型的基础。针对地铁基坑降水问题,在国内对上海地区的研究程度比较高,如骆祖江等曾经对上海第四纪沉积层岩土工程特性进行了研究[1]。在基坑渗流计算方面,吴林高等人将渗流理论与工程实践相结合,解决了众多的工程地下水问题[2,3]; 俞洪良等人基于二维有限元方法对基坑施工不同阶段地下水渗流特征进行了分析[4]。Wang 等人采用二维有限元方法研究水力挡土墙附近的渗流特征[5]。Wang 等根据深基坑工程围护结构入土深度与降水管井滤管位置及组合关系,结合降水数值模拟结果,优化基坑降水方案,就上海地铁 9 号线宜山路地铁站承压含水层降水提出了多种比选方案[6],对于有效控制周边环境的地面沉降起到了良好的效果。Zhou 等以上海地铁 10 号线航中路地铁站为例,采用三维有限差分法对围护结构不同深度基坑降水进行数值模拟[7],使基坑围护结构设计得到了优化。张叶青、李福清等则针对具体工程成功应用数值方法进行了分析[8,9]。
本文以上海地铁 11 号线徐家汇车站深基坑降水工程为例进行数值计算,通过单孔和群孔抽水试验确定含水层水文地质参数,以此模拟降水期间基坑内外地下水位分布,达到优化降水方案设计和有效控制地面沉降的目的。
2 工程背景
上海地铁 11 号线徐家汇站位于上海市最繁华地段徐家汇商业圈,车站宽21. 6 m,全长204. 8 m,车站结构型式、围护型式、开挖深度、施工方法见表1。地铁 11 号线与地铁 9 号线在这里立体交汇,站台呈 L 形相接( 如图 1 所示) ,实现岛 - 岛换乘,并与地铁 1 号线在徐家汇形成三线换乘枢纽站,三个车站围绕港汇广场布置,三条地铁线及港汇广场地下一层空间组成轨道交通换乘和商业人流的集散空间。地铁站周边环境复杂,地下管线密布、人流车流繁忙,场地施工空间有限,对周边环境的影响及地面沉降控制要求均很高。
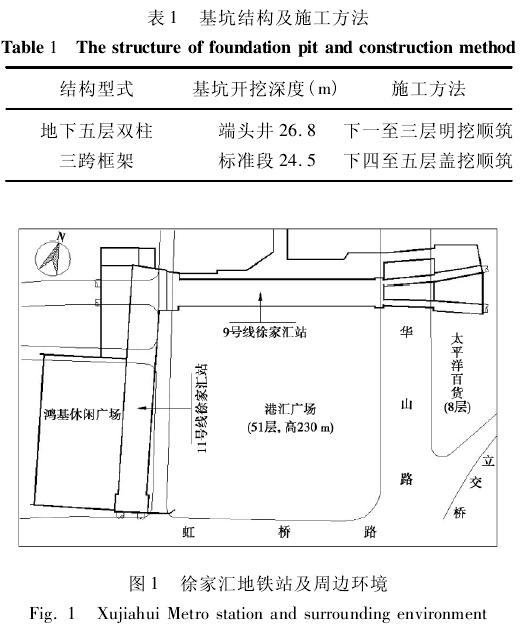
3 场地地质条件
3. 1 地层分布
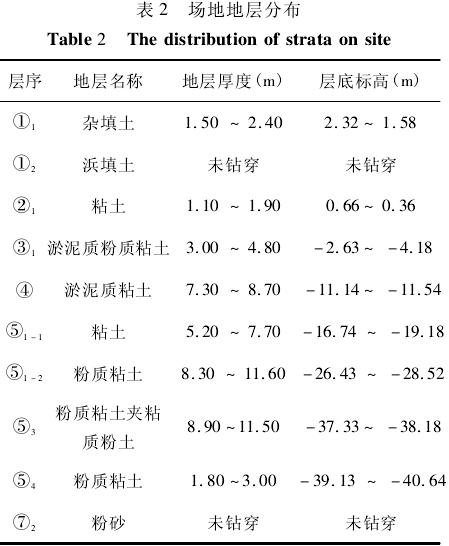
场地地表以下 74. 45 m 深度范围内所揭露的土层均为第四纪松散沉积物,按其成因可分为 7 层( 见表 2) ,其中第④层为灰色淤泥质粘土,流塑、抗剪强度低,具流变和触变特性,也是地铁施工中容易引起沉降和变形的地层; 第⑤层按土层性质及颜色差异又可分为 4 个亚层: ⑤1 - 1、⑤1 - 2、⑤3、⑤4;场地内局部暗浜发育,第⑥层普遍缺失,处于古河道穿过区域,沉积了较厚的第⑤层土; 第⑦1层缺失,第⑦2层粉砂层埋深一般在 45. 0 m 左右。
3. 2 水文地质特征
场地浅部地下水属潜水类型,主要接受大气降水入渗补给,水位随季节而变化,潜水水位约在0. 3 ~ 1. 5 m,按照上海市长期观测资料,年平均地水位埋深一般在 0. 5 ~0. 7 m。场地下部第⑦2层为承压水含水层,具有一定的承压水头,富水性强,承压水水位埋深在9. 0 m 左右,呈年周期性变化规律。
4 地下水渗流模型的建立
4. 1 数值模拟范围与边界条件
根据场地地质条件,结合前人的研究成果和基坑降水实际影响范围观测资料,一般设定平面计算范围为基坑周边向外各取 1 000 m,便可消除计算过程中地下水边界效应产生的影响。本次整个计算区域尺寸为 2 314 m ×2 379 m。在垂直方向上,参照岩土工程勘察资料,以地面以下 82. 00 m 深度为界,层位剖分参照场地典型钻孔资料进行,地层分布及渗透系数如表 3 所示。计算时取降水影响范围以外设定为定水头边界。
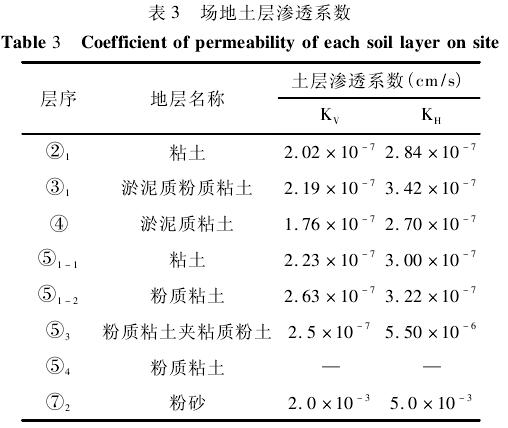
4. 2 模型离散处理
按照计算平面范围及深度、地层分布及初始条件、边界条件,同时考虑抽水井、观测井、止水帷幕在离散模型中的空间位置,结合相关勘察和抽水试验、基坑降水设计资料,对计算区域进行离散,建立三维数值模型。在网格剖分中,对基坑区域范围进行了局部加密,整个模型划分为 16 层,240 行,182列,共 698 880 个单元,如图 2 所示; 在剖面方向上,整个模型共有 7 个参数分区,如图 3。

建立地下水三维渗流计算数值模型之后,先按照抽水试验设计以及初始水文地质参数,进行三维有限差分,通过观测井水位拟合,反演出承压含水层的模型水力学参数,然后再利用反演出的参数进行基坑降水施工三维数值模拟。
5 水文地质参数反演
5. 1 抽水试验
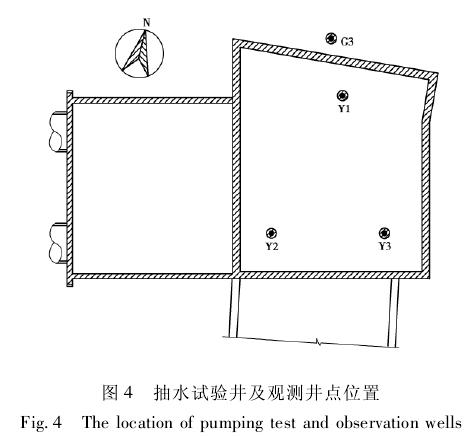
抽水试验在地铁 9 号线和 11 号线徐家汇站共用端头井基坑内进行( 图 4) ,抽水试验的目标层是⑦2层承压含水层。
进行抽水试验时,先分别以抽水井 Y2 ( 53 m)和 Y3 ( 49 m) 作单孔抽水,其水位降深随时间变化的关系曲线如图 5 和图 6 所示,由此可以确定承压含水层⑦2层的静止水位、降深和单井涌水量 Q,再采用地下水动力学公式[10]计算其影响半径 R;然后以 Y1 ( 49 m) 和 Y3 同时进行抽水试验,得到干扰井抽水情况下的水位降深随时间的变化,如图7 所示。
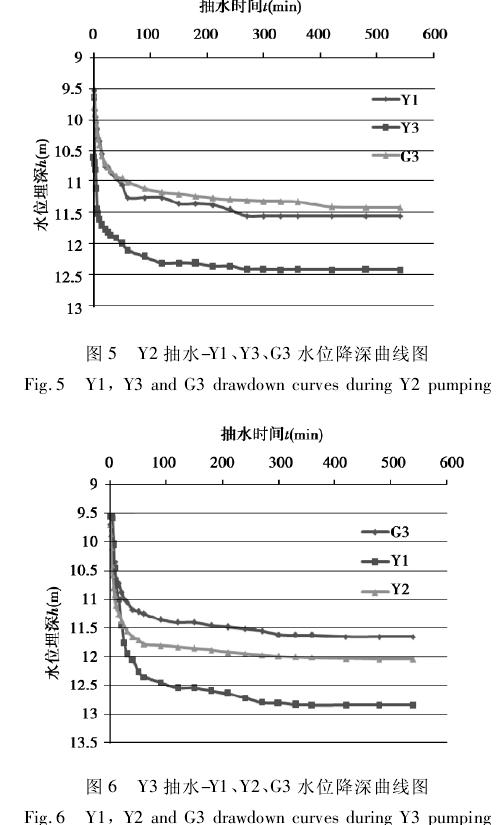
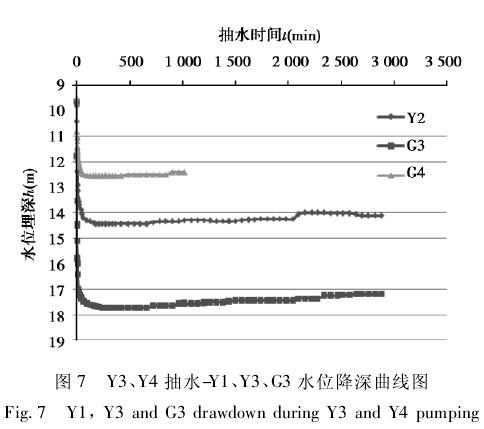
由单孔抽水试验得到 Y2 的平均涌水量为26. 5 m3/ h,Y3 的平均涌水量为 38. 0 m3/ h; 两孔同时抽水期间,Y1 的平均涌水量为 23. 0 m3/ h,Y3 的平均涌水量为 24. 0 m3/ h。由此可见,干扰井孔抽水其单井出水量具有表较明显的减小趋势,且水位降深具有叠加效应。根据抽水井涌水量大小及水位变化值,建立涌水量与水位降深关系,对承压水降水方案进行验证,检验降压降水的效果,评估优化设计方案。
5. 2 水文地质参数反演
多孔介质承压含水层非稳定流三维数学模型可应下述方程表示[7]:
式中: Kxx,Kyy,Kzz分别为沿 x,y,z 坐标轴方向的渗透参数( m/d) ; H 为点( x,y,z) 在 t 时刻水头值( m) ; W 为源汇项( 1/d) ; SS为点( x,y,z) 处的储水率( 1/m) ; t 为时间( h) ; Ω 为立体时间域; Γ2为第二类边界条件; nx为边界 S2的外法线沿 x 轴方向单位矢量; ny为边界 S2的外法线沿 y 轴方向单位矢量; nz为边界 S2的外法线沿 z 轴方向单位矢量;q 为 S2上单位面积的侧向补给量( m3/ d) 。
5. 3 水文地质参数反演数值分析
根据抽水试验结果,选取观测效果比较理想的一组数据进行非稳定流水文地质参数反演。采用Y2 单孔抽水和 G3 观测资料,共选取 20 个数据进行对比分析,反演含水层⑦2层水文地质参数,经过统计分析得出: 最大残差小于 0. 15 m,标准估计误差为 0. 016 m,相关系数 0. 991,说明拟合效果比较理想,符合计算要求。通过三维数值计算反演分析,得到⑦2层的模型参数如表 4 所示。

6 基坑降水运行三维数值分析
6. 1 水文地质参数反演数学模型
基坑降水的目的是为了防止在基坑在开挖过程中产生冒顶和突涌等不良工程现象。要使基坑底板保持稳定必须满足基坑底板至承压含水层顶板间的土压力应大于安全系数下承压水的顶托力。即:
Σ h·γs≥ Fs·γw·H
式中: h 为基坑底至承压含水层顶板间各层土的厚度( m) ; γs为基坑底至承压含水层顶板间各层土的重度( kN/m3) ; H 为高出承压含水层顶板的承压水头高度( m) ; γw为水的重度( kN/m3) ,取 10 kN/m3; Fs是安全系数,一般为 1. 05 ~ 1. 20,本计算取中值 1. 10。
根据现场抽水试验实测结果,承压水水位埋深为 9. 50 m,绝对标高 - 5. 20 m。验算时选取代表性勘探孔揭露的地层作为计算参考,其地面标高为+ 4. 46 m,⑦2层承压含水层顶板标高为 - 39. 54m。安全系数取 1. 10,计算出基坑⑦2层承压含水层承压水的顶托力为:
Fs·γw·H = 1. 1 × 10 × [( - 5. 20) -( - 39. 54) ] = 377. 74 kPa
由此得出地铁 9 号线和 11 号线共用端头井基坑稳定性验算的计算结果如表 5 所示:

根据以上验算结果,结合抽水试验成果,该基坑内共布设14 口降压井,降压井编号为 Y1 ~ Y14,具体井位见图 8。
5. 2 基坑降水运行的三维数值分析
根据开挖工况,采用多点小流量分散降压抽水设置降水井,计算基坑正式降压时周边承压含水层中水位降深,抽水时间按 30 天计算。
共用端头井正式降压过程中考虑采用 Y1、Y2、Y4 作为抽水井,Y3 作为坑内观测井,G3 及 G4作为坑外观测井。正式降压运营过程中,共用端头井降压工况如表 6 所示。正式降压运营中共用端头井要求水位埋深与开挖深度( 标高) 关系曲线如图 10。
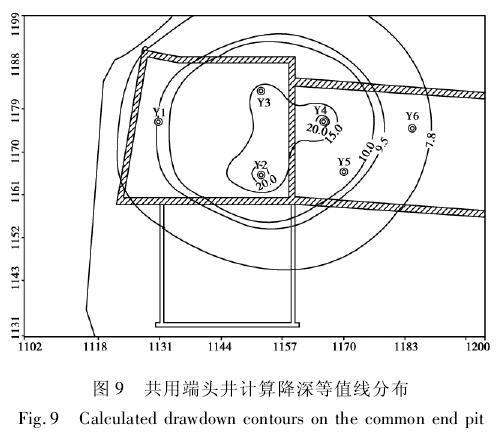
按照以上降水工况进行三维计算,单井出水量根据降压需求进行调整。计算 30 天抽水稳定后 9号线和 11 号线共用端头井第⑦2层降深等值线参见图 9 所示。
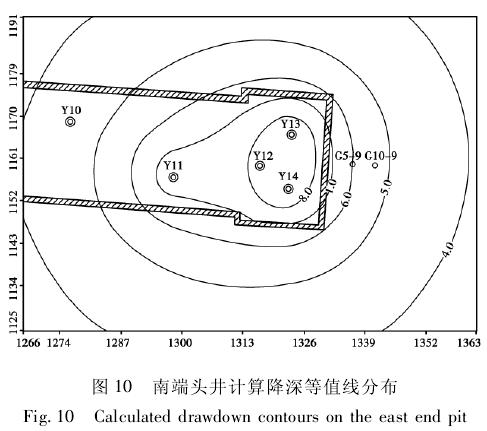
对于南端头井,正式降压过程中考虑采用Y13、Y14 作为抽水井,Y12 作为坑内观测井。计算30 d 抽水稳定后南端头井⑦2层降深等值线参见图 10。
标准段计算降深等值线分布如图 11。
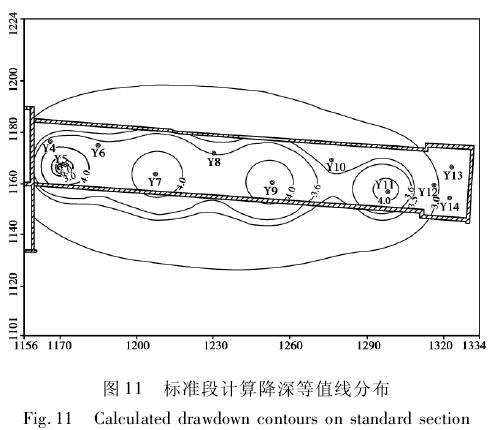
根据开挖工况,标准段及南端头井由南向北进行开挖,因此标准段及南端井开启降压井也考虑由南向北逐步开启及关闭。
7 结语
( 1) 根据室内渗透试验结果和现场抽水试验,对承压含水层( ⑦2层) 进行参数反演的三维数值分析,得出⑦2层模型渗透系数为 Kh= 5. 0 × 10- 3cm / s,Kv= 2. 0 × 10- 3cm / s,二者结果一致,说明室内试验提供的渗透系数参数可靠。
( 2) 数值模拟计算中主要是针对承压含水层⑦2层,在地铁施工中要考虑采用多井小流量抽水降压来控制周边环境影响,在优化抽水运行方案及抽水井流量的情况下,对于共用端头井深基坑减压在 坑 外 5 m 产 生 的 水 位 降 落 最 大 值 达 到了12. 00 m。
( 3) 降水井停抽 15 ~ 30 d 后,根据以往的经验,地面沉降回弹量达到 40 ~50%,后期抽水引起地面沉降反映为非线性叠加。深部沉降量大,浅部沉降量小。在降水施工过程中及降水结束后一段时间内应加强地面沉降及回弹量的监测。
( 4) 为控制或减小基坑降水施工对周边环境的影响,在后期正式降水时应加快施工速度,防止基坑裸露时间过长或降水时间过长,减小沉降的发生。
参考文献(References)
[1] 骆祖江,刘金宝,李朗. 第四纪松散沉积层地下水疏降与地面沉降三维全耦合数值模拟[J]. 岩土工程学报,2008,30( 2) : 193-198. ( Luo Zujiang,Liu Jinbao,Li Lang. Three-dimensional full coupling numerical simulation of groundwater dewatering and land-subsidence in quaternary loose sediments [J]. Chinese Journal of Geotechnical Engineering,2008,30( 2) : 193-198. ( in Chinese) )
[2] 吴林高,刘陕南,李恒仁,等. 工程降水设计施工与基坑渗流理论[M]. 2003,北京: 人民交通出版社. ( Wu Lingao,Liu Shannan,Li Hengren,et al. Design and Execution of Dewatering & Theory of Seepage in Deep Excavation[M]. Beijing: China Communication Press,2003. ( in Chinese) )
[3] 吴林高,李国,方兆昌,等. 基坑工程降水案例[M].北京: 人民交通出版社. 2009. ( Wu Lingao,Li Guo,Fang Zhaochang,et al. Dewatering case History for excavation[M]. Beijing: China Communication Press,2009. ( in Chinese) )
[4] 俞洪良 陆杰峰 李守德. 深基坑工程渗流场特性分析[J]. 浙江大学学报( 理学版) . 2002,29( 5) : 595-600. ( Yu Hongliang,Lu Jiefeng,Li Shoude. Study on seepage field characteristics of foundation pit excavation[J]. Journal of Zhejiang University. ( Science Edition) ,2002,29( 5) : 595-600. ( in Chinese) )
[5] Wang G G,Yan P,Gong X N. Research on the seepage field of excavation with waterproof structure[J]. Ind Constr. 2001,31( 4) : 43-45.
[6] Wang J X,Hu L S,WU L G,et al. Hydraulic barrier function of the underground continuous concrete wall in the pit of Metro station and its optimization[J]. Environmental Geology. 2009,57: 447-453
[7] Zhou Nianqing,Pieter A V,Lou Rongxiang,et al. Numerical simulation of deep foundation pit dewatering and optimization of land subsidence controlling[J]. Engi-
neering Geology. 2010,116( 3-4) : 251-260.
[8] 张叶青,兰韡. 复杂地质越江隧道深基坑减压降水设计与试验[J],山西建筑,2009,35( 33) : 105-106.( Zhang Yeqing,Lan Wei. Pressure reduction dewatering design and test of the cross-river tunnel deep foundation with complex geology[J]. Shanxi Architecture,2009,35
( 33) : 105-106. ( in Chinese) )
[9] 李福清,武永霞,胡向东. 杭州庆春路隧道超深基坑水文地质抽水试验三维有限差分法数值分析[A]/ /地下工程施工与风险防范技术———2007 第三届上海国际隧道工程研讨会文集[C]. 2007. ( Li Fuqing,Wu Yongxia,Hu Xiangdong. The 3D numerical simulation based on finite difference method of the hydrogeologic pumping test in Deep pit of QingChun Road tunnel in Hangzhou[A]/ / Underground Construction and Risk Prevention———Proceedings of the 3rd International Symposium on Tunnelling-Shanghai[C]. 2007. ( in Chinese) )
[10] 薛禹群. 地下水动力学[M]. 1986,北京: 地质出版社. ( Xue Yuqun. Hydrodynamics[M]. Beijing: Geological Publishing House,1986. ( in Chinese) )