多线叠交盾构施工引起土体变形数值模拟
摘 要:针对上海地铁十一号线徐家汇站至上海体育馆站施工区间隧道四线叠交的复杂穿越形式,采用三维有限元方法,模拟了多线叠交盾构隧道施工的整个过程。利用单元生死技术和重复设定单元属性等方法实现土体卸荷、盾构推进、管片拼装以及注浆硬化等动态施工过
程,针对多线叠交盾构施工穿越既有隧道区域所引起的地层变形进行了分析,将得出的数值模拟结果与监测结果进行对比,研究结果表明,地表沉降最大值的位置与盾构机顶推面位置有一定关系; 当两线隧道穿越完成后,地表沉降的最大值位置与单线隧道穿越引起的最大值位置相比会发生一定量的偏移。研究成果可以为多线叠交盾构隧道施工区域保护技术的实施提供一定的理论基础。
关键词: 隧道工程; 盾构法; 多线叠交; 地表沉降; 三维有限元
1 引 言
随着我国城市地铁建设的迅速发展,轨道交通网络的不断完善,城市地下空间开发利用的规模也在不断扩大,软土城区盾构法施工在高速发展的同时也面临着更大挑战,盾构法施工将不断向超深度、急曲线、长距离以及大直径等趋势发展。同时,随着城区土地供求矛盾的日益明显,使得多线叠交以及超长距离叠交盾构施工的现象越来越普遍。盾构法施工时,往往会引起隧道周围地层的土体扰动,从而引起差异沉降,影响既有隧道正常使用。因此,针对工程穿越区域复杂的施工情况,采用三维有限元方法对盾构施工引起的地层变形进行分析是十分有意义的。
Soliman 等( 1993)[1]针对近间距平行隧道进行二维和三维有限元研究,分析了忽略地层损失情况下两隧道相互影响的程度与隧道间距的关系。Addenbrooke 和 Potts( 1996)[2]采用非线性平面有限元模型对双孔隧道施工进行了分析,重点考虑了两隧道平行以及垂直重叠这两种情况。孙钧和刘洪洲( 2002)[3]在考虑注浆和盾尾空隙以及盾构推进所产生的地层损失情况下,采用三维弹塑性有限元,分析了上海地铁交叠盾构隧道施工变形问题。张海波等( 2005)[4]采用三维非线性有限元,针对近距离叠交情况下后建隧道盾构施工引起既有隧道衬砌的应力和变形进行了模拟。Chehade 和Shahrour( 2008)[5]采用平面有限元模型分析了双孔隧道施工中的相互作用,重点考虑了隧道的三种相互位置( 水平排列、斜向排列和垂直排列) 以及施工先后顺序所产生的影响。王渭明和路林海( 2009)[6]针对青岛市台东站近距离叠交隧道施工,采用三维数值仿真技术,研究了施工时引起的地表沉降以及上下隧道交互影响变形规律。陶连金等( 2009)[7]以北京地铁盾构近接工程为背景,通过现场监测以及理论分析,探讨了新建盾构隧道施工对既有盾构隧道纵、横向变位、附加弯矩及轴力的影响变化规律。胡群芳和黄宏伟( 2006)[8]通过对上海 M4 线张扬路至浦电路区间隧道近距离下穿越已运营 M2 线工程施工过程的监测,分析对比了盾构两次近距离下穿越施工的过程和特点。
目前,国内外学者针对软土地区盾构施工引起的地层变形进行了较为丰富的研究[9 ~11],但对于控制盾构施工对既有隧道变形影响的研究相对较少,特别是多线及较长距离叠交隧道之间的相互影响规律以及所引起周围地层变形规律的理论研究极其匮乏。本文以上海地铁十一号线徐家汇站至上海体育馆站施工区间为背景,采用三维有限元方法将复杂的四线倾斜叠交穿越形式建立模型,分析多线叠交盾构隧道穿越施工所引起的地层变形,得出了地表沉隆与施工工况以及隧道位置之间的关系,对地铁设计、施工、灾害防治以及城市地下空间的开发利用都具有理论研究和实践指导意义。
2 工程简介
盾构推进区间为上海市轨道交通十一号线北段二期徐家汇站至上海体育馆站区间隧道,如图 1所示。隧道施工过程中,上海地铁十一号线上行线将先从下方穿越营运中的轨交四号线,然后下行线从上方穿越叠交隧道。从上方穿越四号线,形成四线隧道叠交的特殊工况。
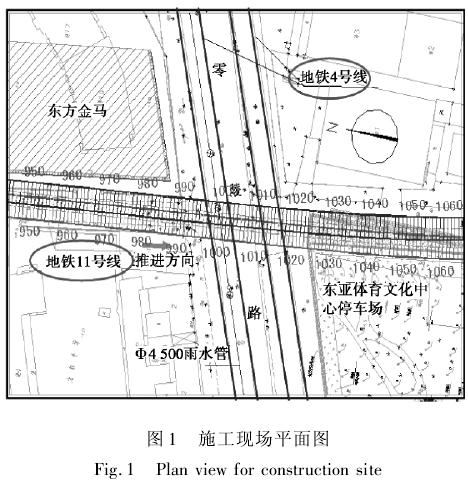
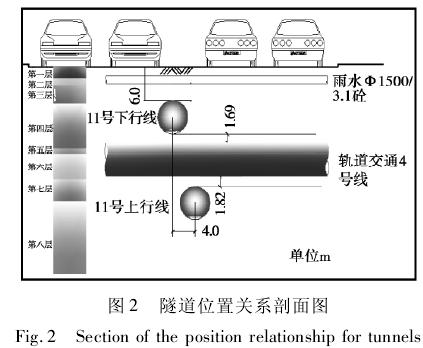
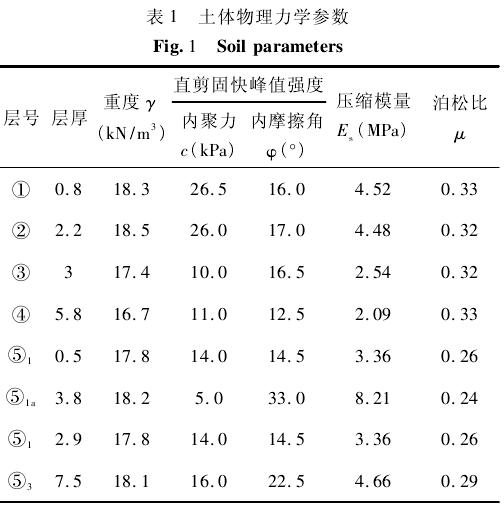
上行线从四号线隧道下部穿越,盾构与四号线隧道竖向净距为 1. 82 m,下行线从四号线隧道上部穿越,盾构与四号线隧道竖向净距为 1. 69 m,盾构四号线,形成四线隧道叠交的特殊工况。同时,两施工隧道的叠交距离将达 965 m,为较长距离的叠顶覆土深度约为 6. 0 m,如图 2 所示。穿越区域涉及到的各主要土层物理力学性质指标见表 1所示。
3 数值模拟结果与分析
3. 1 计算模型
三维有限元计算模型如图 3 所示。整个模型z 方向长为 120 m,设为深度方向,共有 8 层土,y 方向为沿十一号,长为 144 m,x 方向为垂直十一号线方向,长为 95 m。模型上表面为地表,取为自由表面,侧面为位移边界,限制水平移动,底部为固定边界,限制水平移动和垂直移动。

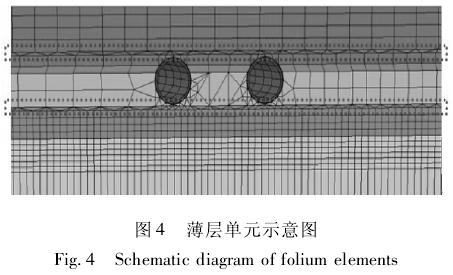
由于在实际工程中,本区间隧道与轨交四号线既不平行施工,也不垂直施工,而是呈现约 75°夹角进行斜交穿越施工,这不仅给施工带来了巨大风险和挑战,同时也给数值模型的建立带来了较大困难。为了实现不同区域的节点耦合,在四号线所在区域与十一号线上行线所在区域之间以及四号线所在区域与十一号线下行线所在区域之间各设置了一层特殊的薄层单元,如图 4 所示。
3. 2 模拟步骤
首先对模型土体进行地应力平衡,使模型处于有地应力而无位移的状态,平衡后位移的量级保持在 10- 4m 即可认为是达到平衡,隧道盾构动态施工整个过程的模拟是将盾构跳跃式向前推进作为一个非连续过程来研究,在有限元软件中采用改变单元材料类型的方法来实现,也就是采用刚度迁移法来完成模拟,即将盾构向前推进看成刚度和载荷的迁移过程。实际操作过程中,在盾构机壳和管片周围土体扰动带均设有预制单元,开挖面推进时,盾构机壳逐渐深入,土体扰动带的单元刚度降低到很小,随后注浆体的硬度逐渐发生变化,另外衬砌的支护开始作用,这种情况下激活预先设置的死单元来实现其作用。模拟盾构开挖的整个过程如图5 所示。
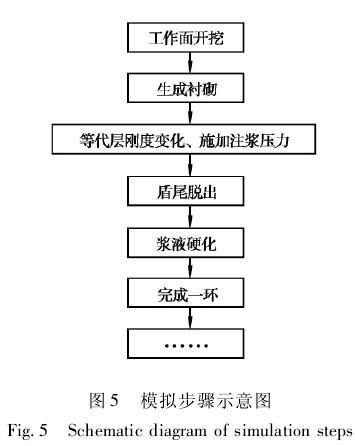
3. 3 结果分析
以十一号线上行线盾构开挖引起的上行线第955 环处上方横向地表沉降和第 1 000 环处上方横向地表沉降为研究对象,以及下行线第 959 环和第1 004 环处上方横向地表沉降为研究对象。对比分析了盾构施工引起的不同区域的横向地表沉降差异,其开挖方向和选取的研究范围如图 6 所示。

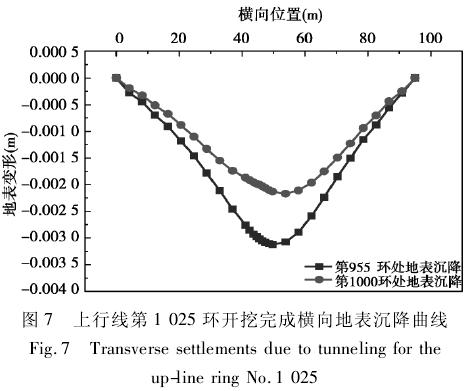
( 1) 上行线开挖完成时横向地表沉降分析: 从图 7 可以看出,当上行线第 1 025 环开挖完成时,地表发生沉降,上行线第 955 环正上方地表最大沉降为 3. 2 mm,上行线第 1 000 环处地表正上方沉降量为2. 0 mm,第1 000 环和第955 环上方地表的最大沉降量差值为 1. 2 mm。第 955 环和第 1 000环处隧道两侧的地表沉降量随着距隧道轴线的远离呈递减趋势,在距隧道轴线 45 m 处的地表沉降已趋近于 0. 25 mm。
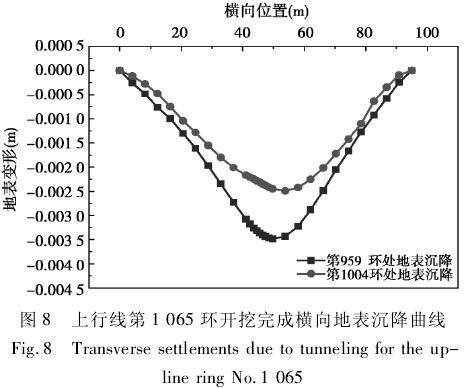
从图 8 中可以得出,当上行线第 1 065 环开挖完成时,整个地表的沉降量进一步增大,但增大的幅值相对较小,上行线隧道第 955 环正上方地表最大沉降量为 3. 5 mm,上行线第 1 000 环处地表正上方沉降量增大到2. 4 mm,第1 000 环和第955 环上方地表的最大沉降量差值趋于平稳,其差值为1. 1 mm。
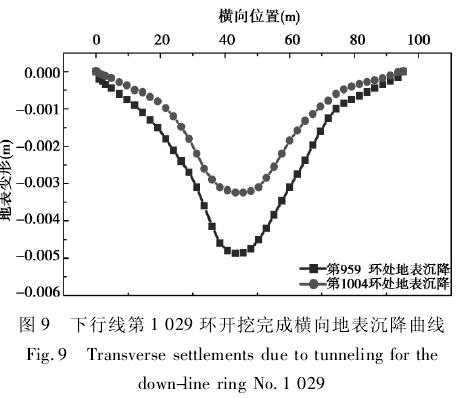
( 2) 下行线开挖完成时横向地表沉降分析: 由图 9 可知,当下行线第 1 029 环开挖完成时,整个地表沉降量在原有基础上增大,下行线隧道第 959环处正上方地表最大沉降为 4. 9 mm,下行线第1 004环处地表正上方沉降量增大到 3. 2 mm,第 1004 环和第 959 环上方地表的最大沉降量差值开始减小,其差值减小到 1. 7 mm。
由图 10 可见,当下行线第 1 069 环开挖完成图 10 下行线第 1 069 环开挖完成横向地表沉降曲线时,整个地表的沉降量相对之前进一步增大,但增大幅值相对较小,下行线隧道第 959 环正上方地表最大沉降量为 5. 11 mm,下行线第 1 004 环处地表正上方沉降量增大到 4. 65 mm,两者之间的差值进一步减小,其值为 0. 5 mm。
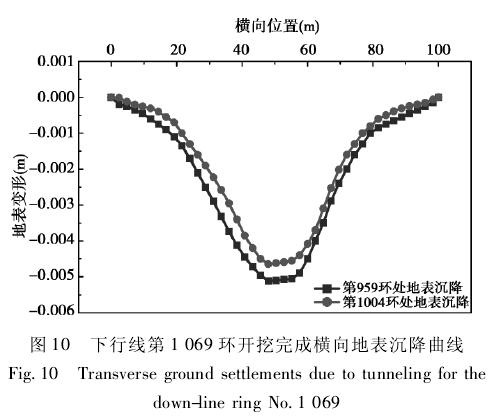
( 3) 纵向地表沉降分析: 为了对比分析盾构施工穿越叠交区段以及非叠交区段所引起的纵向地表沉降差异,本模型在模拟十一号线上行线盾构开挖过程中,选取盾构施工推进试验段上行线第 1065 环开挖时隧道轴线正上方纵向地表沉降以及下行线 1 069 环开挖时隧道轴线正上方纵向地表沉降为研究对象,进行沉降差异对比分析,其数值模拟提取的纵向地表沉降值位置如图 11 所示。在曲线图中,取模型纵向地表方向为 x 轴,深度方向为 y 轴,开挖起始点为坐标原点。

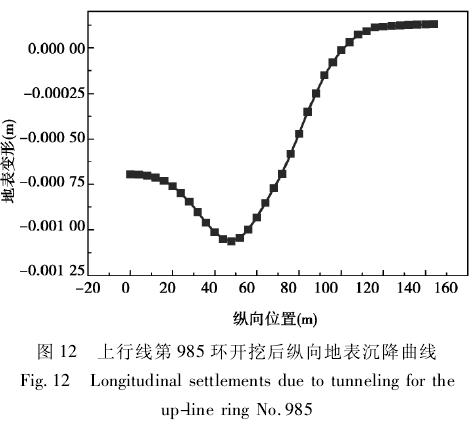
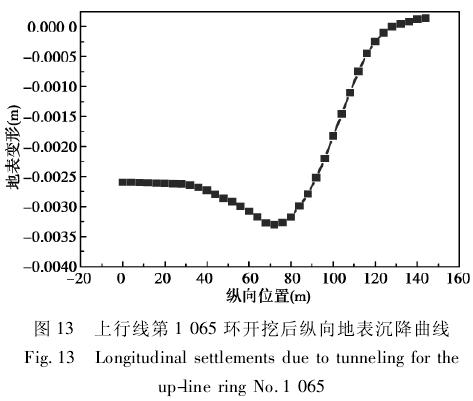
由图 12 可见,当上行线第 985 环开挖完成时,整个地表的沉降量开始增大,由上行线盾构开挖引起的地表最大沉降发生在第 980 环隧道轴线正上方,其值为 1. 06 mm,从图 13 可见,当上行线第 1 065 环开挖完成时,由上行线盾构开挖引起的地表最大沉降发生在第 1 005 环隧道轴线正上方,图 13 上行线第 1 065 环开挖后纵向地表沉降曲线其值为 3. 2mm。沿盾构掘进方向,从第 950 环到968 环处地表沉降量趋于稳定,其值为 2. 53 mm;第 1 052 环正上方地表沉降量趋于稳定,其值为0. 14 mm。
4 监测结果对比分析
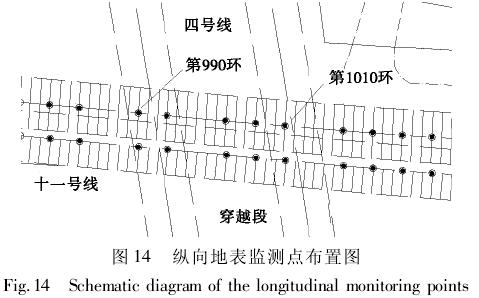
根据本工程施工的特点和相对位置设计,综合其他各种因素,以十一号线上下行线穿越四号线上下行线中心向外各延伸 60 m 作为监测范围,如图14 所示,利用自动沉降采集系统以及常规光学测量仪器进行监测。
地铁十一号线上行线盾构推进到第1 070 环,十一号线上行线盾构下穿四号线区段施工已完成,选择 2010 年 6 月 30 日 7: 00 时刻监测到的十一号线上行线轴线正上方地表沉降值与有限元模拟计算值进行了对比分析,如表 2 所示。
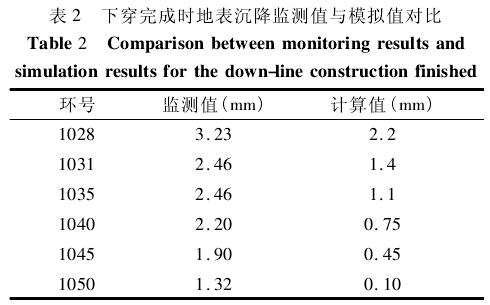
由表 2 可见,以十一号线上行线下穿完成时地表沉降监测值与模拟计算值对比结果为例,两者最大差值发生在现场环号 1 040 环和 1 045 环处,相差 1. 45 mm; 在现场环号 1 028 环处两者差值最小,相差 1. 03 mm; 两者所反映的整体变化趋势相同,即沉降量均随着隧道环号的增加呈逐步减小的趋势。
5 结论
结合上海地铁十一号线徐家汇至上海体育馆区间盾构隧道施工,采用三维有限元法,针对隧道施工过程中的地表沉隆进行了分析,探讨了盾构施工所引起的地层变形影响。主要有以下几点结论:
( 1) 当上行线单线开挖完成后,地表沉降最大点位于其轴线正上方,当两线隧道穿越完成后,地表沉降的最大值位置与单线隧道穿越引起的最值位置相比会发生一定量的偏移,位于上行线和下行线轴线之间。
( 2) 地表的纵向沉降与盾构施工时盾构机顶推面的位置有关,在顶推面前方,土体受到盾构机的挤压,会发生隆起的现象,而在顶推面的后方,土体受到不同程度地扰动,同时受到重力场的作用,发生下沉。此外,地表沉降峰值点的位置也会随着开挖的进行,一直往前平移。
( 3) 十一号线上行线下穿完成时,十一号线上行线轴线正上方地表沉降监测值与有限元模拟计算的沉降值两者所反映的整体趋势相同,两者产生的最大沉降均发生在叠交区段; 离叠交区段越远,监测沉降值和计算沉降值越小。
参考文献(References)
[1] Soliman E,Duddeek H,Ahrens H. Two and three-dimensional analysis of closely spaced double-tube tunnels[J]. Tunneling and Underground Space Technology,1993,8( 1) : 13-18.
[2] Addenbrooke T I,Potts D M. Twin tunnel interaction:surface and subsurface effects[J]. International Journal of Geomechanics,2001,1( 2) : 249-271.
[3] 孙钧,刘洪洲. 交叠隧道盾构法施工土体变形的三维数值模拟[J]. 同济大学学报,2002,22( 4) : 379-385. ( Sun Jun,Liu Hongzhou. 3-D numerical simulation of ground surface settlement under overlapped Shield Tunneling [J]. Journal of Tongji University,2002,22( 4) : 379-385. ( in Chinese) )
[4] 张海波,殷宗泽,朱俊高. 近距离叠交隧道盾构施工对老隧道影响的数值模拟[J]. 岩土力学,2005,26( 2 ) : 282-286. ( Zhang Haibo,Yin Zongze,Zhu Jungao. Numerical simulation of influence of new tunnel on short distance overlapped old tunnel during shield tunneling[J]. Rock and Soil Mechanics,2005,26( 2) : 282-286. ( in Chinese) )
[5] Chehade F H,Shahrour I. Numerical analysis of the interaction between twin-tunnels: influence of the relative position and construction procedure[J]. Tunneling and Underground Space Technology,2008,23( 2) : 210-214.
[6] 王渭明,路林海. 台东交叠隧道施工过程数值分析[J]. 地下空间与工程学报,2009,5( 6) : 1 181-1 187. ( Wang Weiming,Lu Linhai. Numerical analysis of excavation process of the overlapping Tunnels at Taidong Station of Qingdao City[J]. Chinese Journal of Underground Space and Engineering,2009,5( 6) : 1 181-1 187. ( in Chinese) )
[7] 陶连金,孙斌,李晓霖. 超近距离双孔并行盾构施工的相互影响分析[J]. 岩石力学与工程学报,2009,28( 9) : 1 856-1 862. ( Tao Lianjin,Sun Bin,Li Xiaolin. Interaction analysis of double holes extremely close approaching parallel shield tunnels construction[J]. Chinese Journal of Rock Mechanics and Engineering. 2009,28( 9) : 2 856-1 862. ( in Chinese) )
[8] 胡群芳,黄宏伟. 盾构下穿越已运营隧道施工监测与技术分析[J]. 岩土工程学报,2006,28( 1) : 42-47. ( Hu Qunfang,Huang Hongwei. Analysis and monitoring on shield tunneling under existing adjacent tunnel[J]. Chinese Journal of Geotechnical Engineering.2006,28( 1) : 42-47. ( in Chinese) )
[9] 孙 阳,沈水龙,关战伟. 水平旋喷加固盾构进出洞口三维有限元分析技术分析[J]. 地下空间与工程学 报, 2011, 7 ( 1 ) : 65-69. ( Sun Yang, Shen Shuilong,Guan Zhanwei. Three-dimensional finite element analysis on reinforcement of entrance and exit for shield by horizontal jet grouting[J]. Chinese Journal of Underground Space and Engineerjing. 2011,7( 1) : 65-69. ( in Chinese) )
[10] 蒋明镜,王富周,朱合华. 考虑尾隙的盾构隧道土压力离散元数值分析[J]. 地下空间与工程学报,2010,6 ( 1) : 28-32. ( Jiang Mingjing,Wang Fuzhou,Zhu Hehua. Numerical Simulation on earth pressure for shield tunnels incorporating tail gaps by DEM[J]. Chinese Journal of Underground Space and Engineerjing.2010,6( 1) : 28-32. ( in Chinese) )
[11] 陈宇,朱继文. 双圆盾构隧道的流固耦合分析. 地下空间与工程学报[J]. 2010,6( 1) : 21-27. ( Chen Yu,Zhu Jiwen. Coupled fluid-mechanical analysis of Dot shield tunnel[J]. Chinese Journal of Underground Space and Engineerjing. 2010,6( 1) : 21-27. ( in Chinese) )