爆炸冲击波在地铁车站内的传播规律研究
摘 要:地铁是重要的生命线工程,具有造价高、使用周期长、运行期间内部人员密集等特点,极易成为恐怖爆炸袭击的目标。为了使地铁车站在遭受爆炸恐怖袭击时不至于造成严重破坏,利用三维数值分析软件 LS-DYNA3D 建立了地铁车站的数值计算模型,并对其内爆炸效应进行了分析和研究,得到了爆炸冲击波在地铁车站内的传播规律。研究结果表明,炸药在封闭的空间爆炸产生的峰值超压持续时间和对作用物的破坏程度要比在大气中爆炸效果更明显,其危害也更大,这为地铁车站结构应对恐怖爆炸袭击应急预案的制定提供了依据。
关键词: 地铁车站; 恐怖爆炸; 传播规律; 压强曲线
1 引 言
地铁交通自诞生以来,得到了人们的广泛重视,并随着城市化的进程得到了迅速发展。二十一世纪城市人口的持续增加和经济的迅速发展,致使车辆增多,给城市带来了交通拥挤、环境污染与能源危机等一系列问题。地铁作为缓解城市交通紧张的有效工具,在许多国家和城市得到了广泛的应用。随着我国国民经济的飞速发展,城市化进程的加速,城市流动人口的增加,大城市的交通状况必将会进一步恶化,而地铁以其自身的独特性,成为缓解城市交通压力的有力工具,当前地铁建设热潮正在全国各大城市踊跃掀起。
当今世界,恐怖活动日益频繁,对国际社会造成了严重威胁。在众多的恐怖活动中,爆炸恐怖袭击已成为当今恐怖分子最常用的恐怖破坏形式[1]。从 1998 年到 2003 年,全球共发生 181 起针对地铁的爆炸恐怖袭击事件,总共造成 431 人死亡和数千人受伤。由于城市地铁人群密集,环境封闭,一旦发生爆炸袭击事件,结构会在爆炸荷载作用下产生强烈的动力响应发生破坏,甚至是整体连续性倒塌。另外,爆炸冲击引起的地面振动也有可能引起周边地面建筑物的破坏和倒塌,这将严重威胁人民的生命财产安全。
P. C. Chan 和 H. H. Klein 采用三维 Euler 模拟技术,对正平行六面体内形心处装药爆炸而产生的压力场进行了数值模拟[2]; 杨科之和杨秀敏等采用三维爆炸流场计算程序对坑道中的爆炸效应进行了数值模拟[3]; 彭道富和李忠献等对爆炸荷载作用下既有隧道结构的稳定性进行了数值分析[4]。地铁车站是一个密闭的地下结构,内部结构复杂,结构构件类型繁多[5],因此,开展地铁车站应对恐怖爆炸袭击的防护技术研究,探讨爆炸冲击波在地铁车站内的传播规律已成为一项迫切需要解决的课题。
2 数值计算模型的建立
本文将利用有限元动力学软件 LS-DYNA3D,采用流固耦合分析方法来研究爆炸波在地铁车站内的传播规律。建立地铁车站三维模型,研究爆炸波在车站结构内的传播过程,对爆炸波在内部的传播进行动态模拟显示,找出爆炸超压和质点速度、加速度在纵向和竖向的衰减规律。
炸药的材料模型采用 MAT_HIGH_EXPLOSIVE_BURN 材料模型,爆轰压力 P 和单位体积内能及相对体积 V 的关系采用 JWL 状态方程加以描述。空气的材料模型采用 MAT_NULL 材料模型和线性多项式状态方程 EOS_ LINEAR_ POLYNOMIAL 描述。为了描述混凝土的非线性变形及断裂特性,在计算 中 衬 砌 材 料 模 型 选 用 MAT JOHNSON HOLMGUIST CONCRETE 材料模型,材料编号为111,对所选取的经验公式进行数值模拟和评估。周围土体材料模型采用 MAT_SOIL_AND_FOAM。
假设空气、炸药为均匀连续介质,整个爆炸过程为绝热过程。采用的立方体 20 cm × 20 cm ×20 cm TNT 装药,炸药的 TNT 等效当量为 15 kg。在建立有限元模型时,混凝土地面采用 Lagrange 单元,空气和炸药采用 Euler 单元,然后采用 LS-DY-NA3D 提供的 CONSTRAINED_ LAGRANGE _IN _SOLID 约束条件使 Euler 单元与 Lagrange 单元发生作用。具体建模时考虑到问题的对称性,取 1/4模型进行简化计算,在 1/4 模型下炸药的体积为10 cm × 20 cm × 10 cm,假定 TNT 炸药离地面100 cm,中心起爆,爆炸中心离地面 110 cm,对称面上采用对称边界条件,混凝土地面和空气除对称 面的其余各面均采用无反射边界条件以反映无穷大介质。
车站总长度为 16 m,站台结构层净高 4. 8 m,轨道处结构层净高 6 m,站台宽 l2 m,衬砌厚度为0. 8 m,根据对称性取 1 /2 建模。车站结构横截面如图 1 所示。
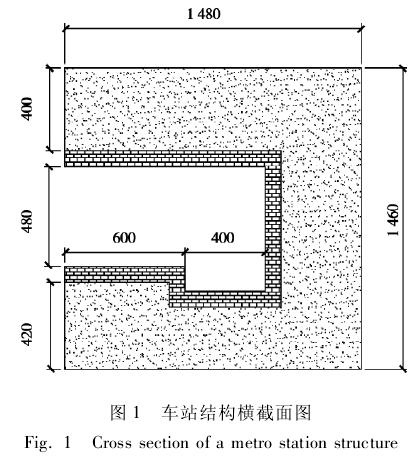
3 爆炸冲击波的传播规律
炸药在地铁车站内部发生爆炸时,由于所处地下空间的半封闭性、截面不规则性等特点,这使得爆炸波在地铁车站内爆炸后形成的空气流场极为复杂[6]。本文利用软件对计算结果进行了后处理分析,并且对爆炸波在空气中传播以及引起的空气压强分布进行了可视化显示。如图 2 所示,不同时刻空气压强分布的可视化显示,其能帮助我们更好地理解爆炸波在地铁车站的复杂环境中的传播过程。
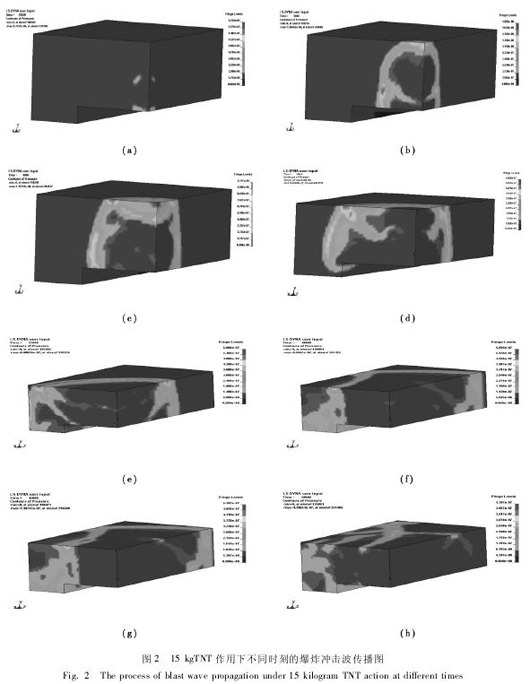
通过对上述爆炸冲击波传播过程的动态显示进行分析,可以得出:
( 1) 爆炸物起爆后,在没有碰到障碍物前,首先会形成一个球形的爆炸冲击波阵面,并迅速的向外扩张,与此同时冲击波压强也在不断降低;
( 2) 由于爆炸物在距离地铁站台地面 1. 0 m处,因此爆炸冲击波在遇到地面时,要受到刚性地面的反射,并且反射冲击波与刚才削弱的正射冲击波叠加,使得距离地面处的冲击波超压被消散减慢;
( 3) 爆炸冲击波继续向四周扩散,冲击波压强也随之降低。当遇到障碍物,尤其是车站顶板处,冲击波会产生来回反射,这使得冲击波波峰的压强持续很高的水平,减弱比较缓慢; 通过与障碍物的接触,入射波和反射波不断叠加,其波形变得不规则,直到充斥整个地铁车站空间。
( 4) 爆炸冲击波在未遇到障碍物时,基本上呈现近似规则的球型或半球型锋面。
( 5) 由于爆炸冲击波在上下结构层以及侧壁的来回反射,反射波与入射波、反射波与反射波多次叠加,使得结构内部各点处都受到多次冲击波压强峰值的作用,并且压强峰值的大小、冲击波的到达时间和作用时间都很复杂。
通过选取地铁车站横向、纵向、竖向三个方向不同距离的爆炸点为参考点,分析研究爆炸波对其作用时空气压力的变化,然后对这些参考点的压力进行分析比较[7]。
横向每隔 2. 0 m 取一个参考点,共取5 个参考点,编号分别为 x -1,x -2,x -3,x -4 和 x -5,它们在地铁车站内的位置,与爆炸点相对位置及爆心横断面所选参考点的压强时程曲线如图 3 所示。

通过比较不同距离不同参考点处的爆炸压强时程曲线可以看出,离爆炸点越近的参考点,其所经历的压强峰值越少,相反,离爆炸点越远,其所经历的压强峰值反而较多。在参考点 x - 1 和 x - 2处,当爆炸冲击波经过时,会出现一个较大的峰值超压,冲击波过后,超压值迅速减弱,最终趋于零;在参考点 x -3 处,当第一个峰值超压经过后,压强会出现小的波动,且波动不明显; 而后又经历了几个比较明显的压强峰值,并且这些压强峰值都比较大。
由此可见,爆炸波以球面波的形式向四周传播。离爆炸点较近的参考点,在爆炸波锋面经过后,由于结构物和障碍物的反射波还未产生,因此影响相对迟缓,但是第一个峰值超压较大; 离爆炸点较远的 x -4 和 x -5 参考点,当爆炸波的锋面到达时,围结构在参考点 x -4 和 x -5 处,第一个峰值超压过后,物和障碍物的反射波也相继到达,因此会有多个值,而首个爆炸超压较小,可见爆炸能量在传播的过程中被消散[8]。
纵向每隔 3. 0 m 取一个参考点,共取5 个参考点,编号分别为 z -1,z - 2,z - 3,z - 4 和 z - 5,它们在地铁车站内的位置,与爆炸点相对位置及纵向所选参考点处的压强时程曲线如图 4 所示。
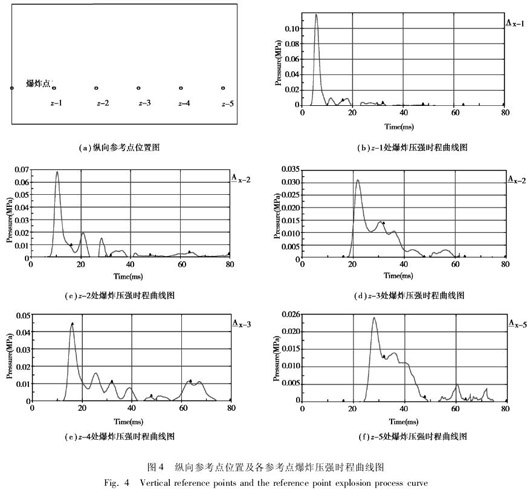
通过比较不同距离不同参考点处的爆炸压强时程曲线我们可以看出,各个参考点都经历了多个压强峰值,并且距离爆炸点越近的参考点,爆炸波对其产生冲击波的波峰越显著,其他的峰值相对较小; 相反,距离爆炸点较远处,各小峰值则相对变大了些。从 z -1 到 z -5,爆炸压强时程曲线类似水波向前推动,随着时间的推移,能量递减,最大波峰值也随之变得越来越小。由此说明,离爆炸点越远,建筑物和障碍物的反射和绕射作用越明显[9]。
纵向不同参考点处的爆炸压强时程曲线与横向相比,有着相似的波形和趋势。
竖向每隔1. 0 m 取一个参考点,共取四个参考点,编号分别为 y -1,y -2,y -3 和 y -4,它们在地铁车站内的位置,与爆炸点相对位置如图 3 所示。竖向所选参考点处的压强时程曲线如图 5 所示。
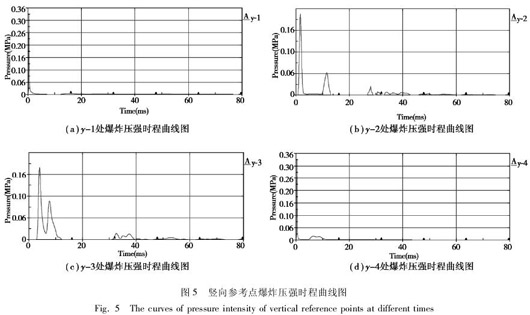
通过比较不同距离不同参考点处的爆炸压强时程曲线图可以看出,当爆炸冲击波的波峰到达该参考点处时,将会产生一个较大的峰值超压,而峰值过后,超压值会逐渐趋于平缓,且没有明显的小波峰出现。这是由于竖向距离较小,各参考点被整个笼罩在爆炸产生的球面波中,因此建筑物和障碍物的反射受影响反而较小[10]。
4 结 论
通过对爆炸冲击波在地铁车站内的传播规律进行分析后,可以得到:
爆炸物起爆后,在没有接触到障碍物之前,首先是以一个比较规则的球形波阵面向前传播,随着时间的推移,能量逐渐消散,冲击波压强也在不断降低; 当遇到结构物或者障碍物后,球形波阵面将发生反射,折射等,经过反射波与入射波、反射波与反射波的多次叠加,结构内部的各点都会受到多次冲击波压强峰值的作用,并且压强峰值的大小、冲击波的到达时间和作用时间都很复杂。由此可以得出: 相同当量的 TNT 炸药在封闭的空间爆炸,其峰值超压持续的时间和对作用物的破坏程度要比在大气中爆炸效果更明显,其危害也更高。
参考文献(References)
[1] 钱七虎. 反爆炸恐怖安全对策[M]. 北京: 科学出版社,2005. ( Qian Qihu. Safety nets dealing terror bombing[M]. Beijing: Science Press,2005. ( in Chinese) )
[2] P. C. Chan,H. H. Klein. Study of blast effects inside an enclosure[J]. Journal of Hluids Engineering Transaction,2004,116( 3) : 450-455.
[3] 杨科之,杨秀敏. 坑道内化爆冲击波的传播规律[J]. 爆炸与冲击,2003,23 ( 1) : 37-40. ( Yang Kezhi,Yang Xiumin. Shock waves propagation inside tunnels[J]. Explosion and Shock Waves,2003,23( 1) : 37-40. ( in Chinese) )
[4] 彭道富,李忠献,杨年华. 爆破动荷载对隧道结构稳定性的影响[J]. 爆破器材,2004,33( 增) : 63-66. ( Peng Daofu, Li Zhongxian, Yang Nianhua.Effects of tunnel structure to explosion[J]. Explosive Materials,2004,33( Supp. ) : 63-66. ( in Chinese) )
[5] Bretislav Janovsky,Petr Selesovskyb,Jan Horkel,et al. Vented confined explosions in Stramberk experimental mine and AutoReaGas simulation [J]. Journal of Loss Prevention in the Process Industries,2006,19( 2-3) : 280-287.
[6] Fernando Diaz Alonso,Enrique Gonzalez Ferradas,Marta Doval Minarro. Consequence analysis by means of characteristic curves to determine the damage to buildings from the detonation of explosive substances as a function of TNT equivalence[J]. Journal of Loss Prevention in the Process Industries,2008,( 21) : 74-81.
[7] 邓国强,周早生,杨秀敏. 爆炸冲击效应数值仿真中的几项关键技术[J]. 系统仿真学报,2005,17( 5) : 1 059-1 062. ( Deng Guoqiang,Zhou Zaosheng,Yang Xiumin. Key technologies of numerical simulation on explosion and impact effect[J]. Acta Simulata Systematica Sinica,2005,17( 5) : 1 059-1 062. ( in Chinese) )
[8] 庞伟宾,何翔,李茂生,等. 空气冲击波在坑道内走时规律的实验研究[J]. 爆炸与冲击,2000,23( 6) :573-576. ( Pang Weibin,He Xiang,Li Maosheng,et al. The formula for airblast time of arrival in tunnel[J]. Explosion and Shock Waves,2000,23( 6) : 573-576. ( in Chinese) )
[9] 李秀地,郑颖人. 坑道中冲击波冲量传播模型的试验[J]. 解放军理工大学学报,2007,( 5) : 425-428.( Li Xiudi,Zheng Yingren. Scale model tests to deter-mine in-tunnel blast impulse from HE-charges at tunnel entrance [J]. Journal of PLA University of Science and Technology( Natural Science Edition) ,2007,( 5) : 425-428. ( in Chinese) )
[10] 都浩,李忠献,郝 洪. 建筑物外部爆炸超压荷载的数值模拟[J]. 解放军理工大学学报,2007,( 8) :413-418. ( Du Hao,Li Zhongxian,Hao Hong. Numerical simulation on blast overpressure loading outside buildings [J]. Journal of PLA University of Science and Technology ( Natural Science Edition ) ,2007,( 8 ) :413-418. ( in Chinese) )