摘　要:结合上海市人民广场地铁换乘大厅枢纽工程,建立了基于黏弹性边界的三维有限元分析模型,利用Newmark数值方法对在拆除临时混凝土支撑振动条件下结构的动力特性进行研究,并将数值计算结果与现场监测结果进行比较.结果表明:所建立的基于黏弹性边界的数值模型不仅能够较好地模拟施工振动下结构的动力特性,消除土体与结构交界面的振动波虚假发射;而且可以预测激励荷载下结构发生共振的可能性.

关键词: 拆撑振动; 地下结构; 黏弹性边界; 动力特性

 

      随着城市建设的发展和城市化进程的不断提高,地下结构的重要性愈显突出^[1].目前,我国许多大城市已建成多条地铁隧道,但修建大规模的地铁换乘大厅还不多见,而且这些地下结构体大多位于繁华的城市商业中心,其施工需围绕绿色施工和工程风险控制的技术开展,需考虑施工振动对周围环境产生的干扰和对结构造成的危害.

      目前,国内外关于施工振动条件下地下结构的动力学研究主要集中于弹性地基梁或结构基础在振动荷载作用下的动力学分析^[2],并通过试验与理论模型相结合的方法得到弹性地基梁等简单结构体在一定假设前提下的动力响应理论解析表达式.但由于地下结构体大多为复杂的空间结构,基于简化假定的解析解存在较大的局限性,为此,改用有限元数值方法进行研究.为了准确模拟结构的动力学特性,所建有限元模型必须如实反映结构构件的几何尺寸和材料特性以及结构与土体之间的相互作用,这就使得有限元模型非常庞大,计算量倍增.

      鉴于此,本文以上海市人民广场地铁换乘大厅枢纽为工程对象,引入黏弹性边界来解决结构与土体界面的虚假反射,从而大幅减少了所建三维分析模型的有限元网格数.同时,采用多种简化单元类型并考虑建模过程中的一些细节问题,根据设计图纸提供的物理特性和材料力学性能参数建立了地铁换乘大厅的空间有限元模型,以期为地下结构设计提供依据.

 

　　上海市人民广场位于繁华的商贸和文化娱乐区域,是上海市重要的行政及公共活动中心,也是近代优秀历史建筑最为集中的区域之一^[3].由于上海市地铁1、2、8号线之间无法满足日换乘量36万人次(预测远期)的设计要求,因此,工程提出了“大三角”换乘大厅的设计施工方案.

      人民广场换乘大厅紧邻地铁1、2号线和联络通道,平面形状为三角形(见图1),总建筑面积约为8 620 m².其顶板覆土厚约0.7~2.0 m,地下1层基坑开挖深度约7.0~9.1 m,局部底板略低于1层,为地下2层结构,基坑开挖深度约14.2 m.为了保证地铁车站的正常运营,围护结构第1道支撑采用钢筋混凝土支撑,并附加局部钢筋混凝土板支撑.工程采用明挖顺作法施工,为了配合九江路交通需求,部分基坑采用盖挖法施工.

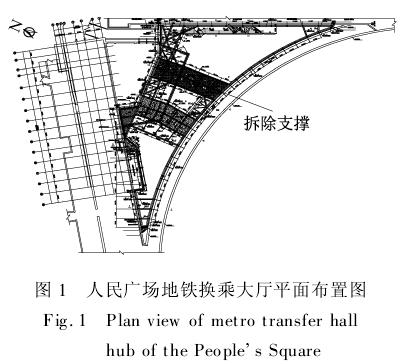
      随着工程的顺利完工,用于施工栈桥的混凝土支撑将被凿除,并选择切割结合镐头机拆除的方案，即先将靠近地铁2号线一侧连接地墙与支撑的围檩切断,然后,利用镐头机向另一侧逐渐推进而进行拆除.由于该工程地处商业闹市区,故需要研究施工拆撑振动下的结构动力特性.

 

　　施工振动模拟采用三维线性动力计算模型,分析对象包括换乘大厅施工场地周围的地下连续墙、底顶板和与地下连续墙相连的钢筋混凝土支撑.采用梁单元模拟梁和柱结构,采用壳单元模拟底顶板、地下连续墙和栈桥桥面.

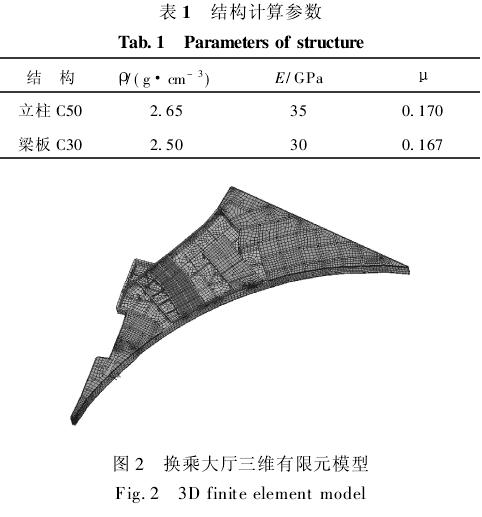
      结构中的立柱按照设计C50混凝土参数选取,其余结构按设计C30混凝土参数选取,所有结构构件的截面形状和尺寸均按照工程施工图进行选取,计算所用结构参数(密度ρ、弹性模量E和泊松比μ)列于表1.图2所示为利用ANSYS软件所建人民广场地铁换乘大厅整体三维有限元模型。

　　计算采用Rayleigh阻尼,根据模态分析^[4-5]确定体系的基频为3.035 Hz,根据经验取其阻尼比为0.05.

      从整体结构来看,结构侧面为地下连续墙,与周围地铁通道和联络通道中的水平梁相连,其连接点处可视为水平绞结,即限制了结构周边水平方向的位移;而在结构底板处,结构与土体相接触.在建立地下结构的三维模型时,通常根据结构的整体空间尺寸而对一定范围的土体进行建模,但将大幅增加有限元的网格总数,且对于尺寸较大的地下空间结构,所建立的土体有限元网格数将更大.考虑到施工振动与地震作用不同(一般为短时间的冲击荷载),可以忽略土体振动对结构的影响而将土体对结构的作用视为弹性约束,采用土弹簧来模拟;但会使得土体与结构界面之间产生振动波的虚假反射,从而造成计算结果的误差.

      为了解决虚假反射的问题,引入黏性边界,即在结构与土体交界处施加单元切向黏性剪切应力σ_n和单元法向黏性压缩应力σ_t,以吸收边界处的反射能量.边界单元处所施加的作用力为

 

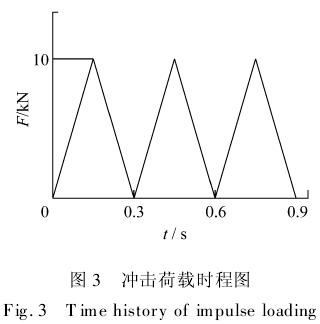
　　在施工振动的数值模拟中,作用在结构上的荷载F包括恒荷载和冲击荷载.恒荷载即为重力,结构的重力按照重力加速度g=9.81 m/s²作为惯性力作用在结构上;冲击荷载为镐头机对钢筋混凝土支撑进行拆除时产生的荷载,并随时间而变化,其大小和频率取决于镐头机的技术参数.本工程镐头机所产生的冲击荷载周期为0.3 s,峰值为10 kN,荷载形式见图3.

　　为了分析结构的振动情况,本文计算了地铁换乘大厅结构的模态振型.其中,模态阶数取为10阶,所得固有频率f见表2.限于篇幅,仅将第1阶模态振型示于图4.

      由表2可以看出:在10 Hz以下,结构具有丰富的模态,特别是在5~6 Hz之间的模态较为密集.从振型上来看,第2、4和5阶模态对施工所要拆除的栈桥影响较大,即在振动过程中,栈桥桥面在竖直方向上摆动,而对结构的其他部位影响较小;第3阶模态对与栈桥连接的地下连续墙影响较大,即在振动时,地下连续墙受到栈桥的拉力作用而向结构内侧弯曲,导致与栈桥连接的地下连续墙附近发生疲劳破坏.因此,在镐头机施工时,应在该部位布置现场监测点,其与理论分析所得结构薄弱点的位置一致.

      此外,镐头机的工作频率约为6.7 Hz,其不在结构的前10阶固有频率范围内,但离结构的第10阶固有频率较近,这对结构构成了很大的危险.一方面,当栈桥上有临时施工设备时,结构固有频率将略有提高,很容易接近6.7 Hz;另一方面,由于工作环境的变化,镐头机的工作频率也会在6.7 Hz上下波动,接近于结构的固有频率,使得结构在激振力的作用下发生共振.因此,施工时有必要进行现场监测.

      为了对结构振动进行深入分析和模拟现场拆撑施工中的结构动力响应,对地铁换乘大厅结构整体进行了冲击荷载作用下的瞬态动力学分析,冲击荷载作用的位置根据现场监测时镐头机作用的位置而定,大致选在与连续墙相连的栈桥支撑梁上,冲击荷载的峰值取10 kN,周期0.3 s,荷载随时间变化的关系曲线见图3,其方向竖直向下.

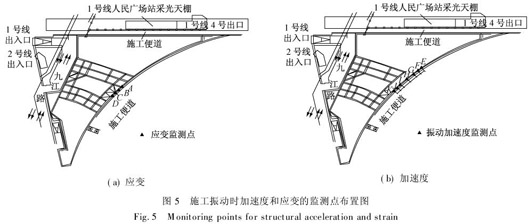
      利用ANSYS结构有限元分析软件进行数值模拟,荷载作用时间取66个循环,约10 s,每个循环取10个子步数,共660个子步数.为了便于对比数值模拟与现场监测的结果,选取结构三维有限元模型中与现场监测点对应的位置进行分析.其中:现场加速度监测点布置在与栈桥端地下连续墙相距1 m的地面上;现场应变监测点布置在与栈桥相连的地下连续墙表面,具体布置见图5.

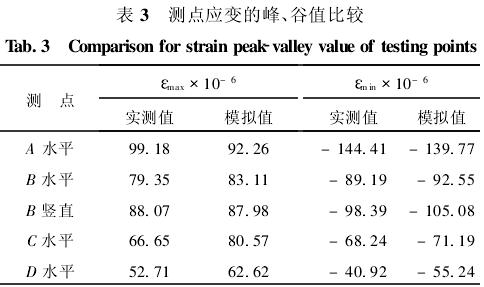
　　各测点的应变测量均在振动源正常工作下进行,但由于现场地墙表面过于粗糙,造成了理论上应测量的2个方向应变无法完成,故只对所能测得的可靠数据进行分析,并将其与数值模拟结果进行对比.现场采集到的可靠应变数据为图5(a)中A、B、C和D点的水平方向及B点的竖直方向.为了便于比较,将实测和模拟的应变的峰值ε_max和谷值ε_min列于表3.由表3可以看出,数值模拟所得应变的峰、谷值与其实测值较吻合,这表明所建立的分析模型及方法能够较好地模拟结构的动力变形特性.

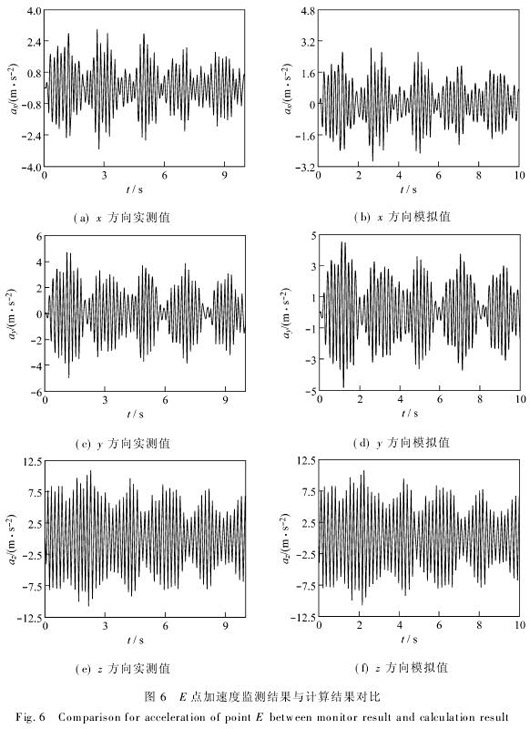
　　将数值模拟的计算结果与现场实测的结果进行对比,以图5(b)中E点为例,将E点的加速度响应时程的实测结果与其计算结果进行对比,其结果见图6.其中,a_x、a_y和a_z分别表示x、y和z方向的加速度.由图6可以看出:E点的实测加速度响应时程曲线与其数值模拟计算的结果基本一致,即两者的波形、幅值与实测结果均基本吻合,各频段的频率组成也基本一致,表明所建立的数值模型能够较好地模拟结构在施工振动过程中的加速度响应规律.

 

　　本文引入了黏弹性边界条件来消除土体与结构交界面的振动波虚假发射,从而缩小了计算模型的网格总数,大幅提高了计算效率.在此基础上,对上海市人民广场三角形换乘大厅进行了三维有限元数值模拟.首先,对结构的动力学模态进行分析,计算结构的固有振型和固有频率,并根据结构前10阶固有振型分析了结构的最薄弱环节;其次,将有限元分析结果与现场的实测结果进行比较.结果表明,两者的结果较吻合,从而验证了所建立数值模型的合理性.所建模型可为该地下结构建立结构健康监测系统,为结构状态的评估提供依据,也可为同类工程的施工和设计提供参考.

 

[1]　高峰.地下结构动力分析若干问题研究[D].重庆:西南交通大学土木工程学院, 2003.

[2]　Yu T X, Chen X W, Chen Y Z. Elastic-plastic beam-on-foundation subjected to mass impact or impulsive loading [ J].Computers and Structures, 2002, 80(26): 1965-1973.

[3]　刘建航,俞加康.上海地铁网络的重要枢纽———人民广场站[J].地下工程与隧道,2006 (1):1-5.

LIU Jian-hang, YU Jia-kang. People Square station———Key juncture in Shanghai metro network [J].Underground Engineering and Tunnels, 2006 (1): 1-5.

[4]　Ojalvo I U. Proper use of Lanczos vectors for large eigenvalue problems: Computers and structures, 1985,20 (1): 115-120.

[5]　曹树谦,张文德,萧龙翔.振动结构模态分析———理论、实验与应用[M].天津:天津大学出版社, 2002.