摘  要　针对实地测试中出现的功率谱异常现象,通过逐项排查,在有限元分析的基础上,发现导致异常现象的根源在于传感器端发生了共振。在有限元数值模拟的基础上提出了一种新的设计方案,并进行了现场对比试验。试验结果表明,功率谱异常现象是结构共振所致,所提出的解决方案保障了振动信号的精密测试。

关键词　振动;实地测试;有限元分析;功率谱密度;地铁

 

      地铁引起的环境振动问题很早就引起了重视,并得到了积极研究。例如:L.G. Kurzweil^[1]根据实测研究了振动与噪声;J.Melke^[2]基于类比分析、实验室测试和实地测试研究了环境振动预测方法;潘昌实等^[3]对北京地铁某区间进行实测获得了动态响应并进行了频谱分析;K. H. Chua等^[4]研究了双隧道地铁对周边建筑物的影响;刘维宁等^[5]依据轨道-砌衬-地层系统给出列车响应模型与振动传播规律,指出了放大区和主要能量频带;王逢朝等^[6]采用车辆-结构-土层-建筑物的二维模型分析地铁振动在地面的传播特性;J.A. Forrest等^[7-8]研究了浮置板的减振效果;闫维明等^[9]根据现场实测数据,对某地铁沿线典型区段地铁引起的地面振动实况和振动特性及其传播规律等进行了分析研究。可见,实地测试已成为研究地铁环境振动的主要手段和重要依据,而测试数据的精度会直接关系到分析结果。笔者针对地铁实际振动测试中出现的谱图异常现象,通过逐层排查和力学分析找出了导致异常现象的力学根源,并在有限元分析基础上提出了相应的解决措施,最后通过实地对比试验验证了方法的有效性和可行性。

 

     地铁振动源强测试的惟一途径是在地铁隧道内进行数据采集,振动污染向环境传播的第一环节也最基础的部分。

      在隧道洞壁振动测试中,得到了如图1所示的结果,其中明显地看到隧道壁测点功率谱在200 Hz和900 Hz附近各有一个峰值,其能量远大于其他频率成分。在对不同列车进行测试时,该现象一直存在,依据力学常识和振动的宽频特性,该现象属于异常现象。

　   针对该异常现象,笔者对测试各个环节进行了逐项检查,最后将注意力集中到了传感器支架上。该支架是在测试洞壁振动时为便于放置传感器而常用的辅助设备,在地铁宽频振动属性下,该支架有可能出现共振问题。笔者对这种可能性进行力学分析。

 

      对于一个N自由度的定常系统,其振动方程为

     

其中:M,C和K分别为轨道结构的总质量矩阵、阻尼矩阵与刚度矩阵;X(t)为系统位移列阵;F(t)为载荷列阵。

      对矩阵M,利用对称Lanczos算法^[10]可产生Krylov子空间K_k(M,v₁)的一组标准正交基v₁,v₂,…,v_k,并且V_k^HMV_k=T_k为对称三对角矩阵。计算T_k的特征值作为M的特征值的近似,并用相应的Ritz向量作为M的特征向量的近似,这就是求解对称矩阵特征值问题的Lanczos方法。Lanczos方法的一个具体应用是Underwood^[11]提出的求解对称矩阵特征值的块Lanczos方法^[12]。

      本次测试用支架长63 mm,宽45 mm,厚3 mm。笔者对测试用支架进行了有限元分析。有限元计算按实物建立3D模型,采用四面体10节点体单元,每个节点有x,y,z三个方向自由度,采用Lagrange多项式插值。

      如图2所示,对应于顶点有

      对应于棱内节点有

　    取单元长度为1 mm,总单元数为112 800。材料常数为:杨氏模量E=2.1×10^11/N/m²;泊松比μ=1/3;密度ρ=7.85×10³kg/m³。

      给定边界条件,约束模型一侧全部节点位移为0,求解分析支架前5阶模态,结果如表1所示。

　   图3自左向右依次所示为传统支架数值,计算结果的第1阶到第3阶振型。

      数值计算结果显示第2阶振型支架中部振动很弱,由于测试时加速度传感器放置于支架中部,所以第2阶振型对于垂直方向影响较小。由于固有频率和振型的综合作用,测试中出现了支架第1阶218Hz和第3阶946 Hz共振带来的显著影响,而第2阶406 Hz的影响并不明显,实测数据中表现为2个尖峰,数值计算结果与实测结果符合较好。

 

      地铁振动测试要求高,工作复杂,为避免仪器选择不当而对测量造成影响,在仪器选取时应该进行设计选择与可靠性测试。

      基于测试要求,为了避免产生共振问题,笔者采用同样的数值计算方法设计了新的防共振支架,并对新支架的性能进行有限元分析。网格剖分图如图4所示。

      新设计的防共振支架前5阶固有频率如表2所示,其第1阶频率为2 597 Hz,前3阶模态如图5所示。

由于地铁振动测试采样频率上限在2 000 Hz,所以防共振支架的设计选取第1阶固有频率下限为2 000 Hz。计算结果显示,新的设计中,传感器放置位置振幅较小且第1阶固有频率足够高,理论验证此设计满足要求。

 

     为验证效果,进行了对比试验。传统测试支架和防共振试验支架被放置于隧道壁上同一点,如图6所示。

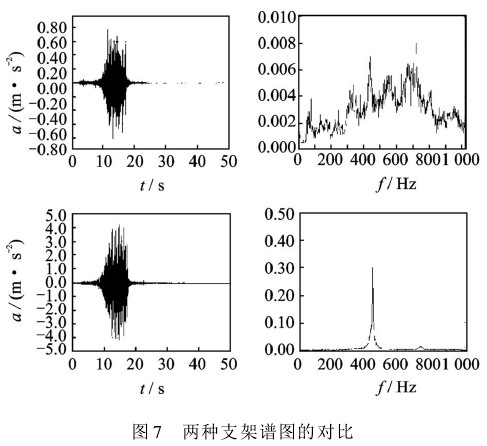
      对比试验结果如图7所示,图中上方为防共振支架测试数据谱图,下方为传统支架测试谱图。对比测试结果可以明显看出,防共振支架在地铁测试采样数据范围内未出现共振现象,而传统支架由于共振在谱图中出现了尖峰,应用新的支架所采集的测试数据准确地反映了地铁振动谱图。

      笔者研究了地铁隧道内振动测试的谱图异常状况,对产生这一现象的原因进行了查找,并根据有限元理论对传统测试的传感器端进行了数值计算。计算结果显示谱图的异常来源于传统测试支架的共振,数值计算结果与试验结果符合较好。以数值计算为基础,设计了新的测试支架,并对传统支架与新的防共振支架进行了对比测试。计算对比测试的振级后发现,由于共振的影响,传统测试支架采集的数据较新支架采集的数据其最大振级大19 dB。支架的共振对测试结果影响很大。通过数值计算的理论检验与实地的对比测试,新设计的支架有效地防止了由于支架共振而对地铁振动测试产生影响。

 

[1]　Kurzweil L G. Ground-borne noise and vibration from underground rail systems[J]. Journal of Sound and Vibration, 1979, 66(3):363-370.

[2]　Melke J. Noise and vibration from underground rail-way lines: proposals for a prediction procedure[J].Journal of Sound and Vibration,1988,120(2):391-406.

[3]　潘昌实,谢正光.地铁区间隧道列车振动测试与分析[J].土木工程学报, 1990, 23(2):21-28.

Pan Changshi, Xie Zhengguang. Measurement and analysis of vibrations caused by passing trains in sub-way running tunnel[J].China Civil Engineering Journal,1990,23(2):21-28. (in Chinese)

[4]　Chua K H, Balendra T, Lo K W. Groundborne vibrations due to trains in tunnels[J]. Earthquake Engineering &Structural Dynamics,1992, 21(5):445-460.

[5]　刘维宁,夏禾,郭文军.地铁列车振动的环境响应[J].岩石力学与工程报,1996(S1):586-593.

Liu Weining,Xia He, Guo Wenjun. Study of vibration effects of underground trains on surrounding environments[J].Chinese Journal of Rock Mechanics and Engineering,1996(S1):586-593. (in Chinese)

[6]　王逢朝,夏禾.地铁列车振动对邻近建筑物的影响[J].北方交通大学学报,1999,23(5):45-48.

Wang Fengchao, Xia He. Vibration effects of subway trains on surrounding buildings[J].Journal of Northern Jiaotong University, 1999, 23 (5): 45-48. (in Chinese)

[7]　Forresta J A, Hunt H E M. Ground vibration generated by trains in underground tunnels[J]. Journal of Sound and Vibration, 2006, 294(4-5):706-736.

[8]　郭亚娟,杨绍普,郭文武.钢弹簧浮置板结构的动力特性分析[J].振动、测试与诊断,2006,26(2):146-150.

Guo Yajuan, Yang Shaopu, Guo Wenwu.Analysis of dynamic characteristics of steel spring supported floating track bed[J].Journal of Vibration, Measurement &Diagnosis,2006,26(2):146-150. (in Chinese)

[9]　闫维明,聂晗,任珉,等.地铁交通引起地面振动的实测与分析[J].铁道科学与工程学报,2006,3(2):1-5.

Yan Weiming, Nie Han, Ren Min, et al.In situ experiment and analysis of ground surface vibration induced by urban subway transit[J].Journal of Railway Science and Engineering,2006,3(2):1-5. (in Chinese)

[10] Lanczos C. An iteration method for the solution of theeigenvalue problem of linear differential and integral operators[J]. Journal of Reserch of the National Bureau of Standars, 1950, 45: 255-282.

[11] Underwood R R. An iterative block Lanczos method for the solution of large sparse symmetric eigenproblems[D]. California:Stanford University, 1975.

[12]杨宇军,陈建军,李维健.具有频率约束的电路板抗振优化设计问题研究[J].振动、测试与诊断,2008,28(1):31-34.

Yang Yujun,Chen Jianjun, Li Weijian. Optimization design of PCB assembly with frequency constraints [J].Journal of Vibration, Measurement &Diagnosis,2008,28(1):31-34. (in Chinese)