摘  要：基于客流需求，特别是高峰客流情况下，地铁线路应配置地铁列车数量问题，建立了地铁线路列车配置数的数学模型，给出地铁线路列车配置数计算方法。以深圳地铁罗宝线的列车配置数及反推数据以及国内部分地铁线路列车配置数据，验证了计算模型的有效性和实用性，同时就如何在地铁实际运营中有效提高列车运能进行了阐述。

关键词：地铁动车组；数量配置；数学模型；运用

 

     地铁列车配置数量的准确计算，不仅是为满足实际客流的需要，同时也是规划、设计车辆段停车能力、维修能力以及人员合理配置数量的重要依据。因此，基于客流需求，建立地铁线路列车配置数的计算模型，在实际地铁设计及运营中具有重要的现实意义。

 

      地铁列车配置分为 2 个部分，一是正线运行列车数；二是库内列车检修、备用数。综合考虑线路长度、列车旅行速度、列车折返时间、列车行车间隔，按照运营 1 个往返周期所需的时间除以行车间隔时间等于运营列车数的思路，建立列车配置数计算模型如下。

      M_配置=M_运营+M_检备， （1）

      M_运营=（2L/V_旅×60+T_{折返 1}+T_{折返 2}）/T_间隔， （2）

      M_检备=M_运营×25%。 （3）

式（1）—式（3）中，M_配置为线路列车配置数；M_运营为线路运营列车数；M_检备为线路库内检修备用列车数；L 为线路全长，km；V_旅为列车平均旅行速度（不考虑折返时间），km/h；T_{折返 1}为始发站折返时间，min；T_{折返 2}为终点站折返时间，min；T_间隔为运营列车行车间隔，m。

      2L/V_旅×60+T_{折返 1}+T_{折返 2}表示按照列车平均旅行速度运行 1 个往返所需要的时间。式（3）为经验公式，检修和备用列车数一般为运营列车数的25%左右，随着检修模式的不同，该比例略有变化。

 

      线路及列车一旦确定，式（1）中的 L、V_旅、T_折返就已经确定，唯一变化的就是 T_间隔。T_间隔主要由 2个因素决定，一是列车载客容量；二是高峰小时单向断面最大客流。

      我国现阶段采用的建标 104—2008 《城市轨道交通工程项目建设标准》中关于站席的规定是，车内面积扣除坐席区及相关设施的面积后，按 6 人/m²核定载客量。实际情况是达不到的，一般按 5 人/m²核定载客量，较为合理。

以深圳地铁罗宝线列车 （6 节编组）为例，按5 人/m²核定载客量，每列车载客容量为 1 608 人。

      以深圳地铁罗宝线为例，2010 年元旦期间，罗宝线高峰小时断面单向客流达到 1.910 7 万人次，2015 年高峰小时单向断面最大客流预计将达到 4.1 万人次。

      由于列车载客能力即每列列车载客容量与开行列车列次的乘积，要满足高峰小时单向断面最大客流的需要，建立行车间隔计算模型如下。

式（4）中，λ 为列车满载率；V_客为高峰小时单向断面最大客流，人次；V 为列车载客容量，人次。

当 λ 大于 1 时，就会出现乘客滞留，因此，需满足 V×（60÷T_间隔）≥V_客，即 T_间隔≤（V×60）/V_客。

 

      以 2010 年深圳地铁罗宝线数据为例，2010 年元旦期间，高峰时期的小时单向断面最大客流达到1.910 7 万人次，每列车载客容量为 1 608 人，列车行车间隔与满载率 λ 关系如图 1 所示。

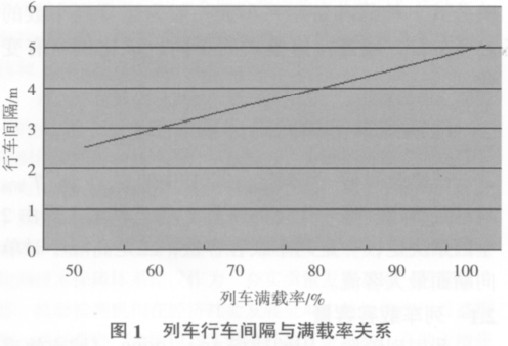
      通过调查获得深圳地铁罗宝线运营的相关参数，见表 1。

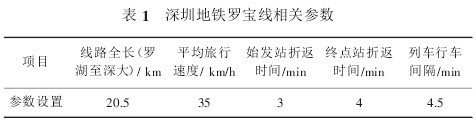
      由模型可计算出罗宝线的地铁列车配置数为21.67 列。2010 年元旦期间，深圳地铁罗宝线实际运营 17 列车，实际共配置 22 列车。可见，通过计算模型计算结果与实际列车配置情况非常吻合。

      由模型计算知，线路配置 22 列车（计算数值向上取整结果），由此可反推检修列车数。

      深圳地铁罗宝线检修作业已趋于成熟，主要修程有大修、架修、年检、三月检和月检。考虑各修程有重叠部分，如每列车的第 3 次月检将改作三月检，因此在反推时需要去除重叠部分。由于一定时间内的检修列车数除以该段时间就等于单位时间内的平均检修列车数，因此可建立反推计算式为

式（5）中，N检修为每工作日检修列车数，列；N年为每年检修列车数，列；T 为完成每列车检修的时间，d；每年以 250 个工作日计。

      由式（5）可计算出各修程检修列车数，见表 2。

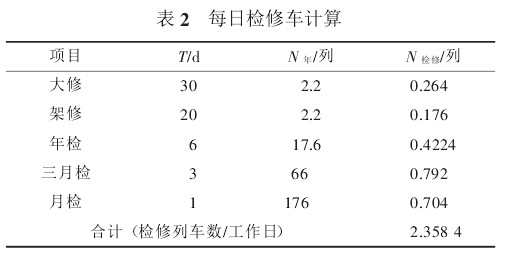
      根据经验，考虑 2 列车备用车，可反推出列车配置数：

M_配置=M_运营+M_检备=17.17+2.358 4+2=21.528 4（列）。

      一般情况下，列车维修均会受生产组织、突发故障等因素影响，因此计算检修车数量时还应考虑生产维修不平衡系数 α（一般取值 1.1）。

M_配置=M_运营+M_检×α+M_备=17.17+2.358 4×1.1+2=21.764 24（列）。

      取整为 22 列，反推出的列车配置数与计算模型一致。

      由于式（3）为经验公式，存在一定误差。因此，通常在根据式（3）计算出列车配置数后，应根据式（5）对检修列车数量进行反推校正，最终得出更为准确的计算结果。

      按照以上建立的计算模型，对国内其他多条地铁线路列车配置数量进行了计算，结果见表 3。

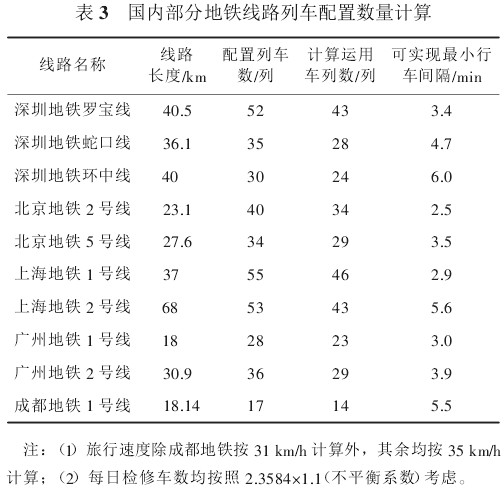
      据调查，发现表 3 计算结果与实际情况基本吻合（由于问题整改、修程修制调整等原因会导致运用车数量发生变化，因而计算结果与实际情况存在一定偏差）。

 

      计算模型对于充分挖掘列车运能具有较强的指导意义，结合深圳地铁在运营管理、既有线新车增购、新线规划及新车采购中的实践经验，总结既有列车配置数下调整、扩大运能的有效手段。

      （1）合理调整行车间隔对于充分利用列车运能具有现实意义。

     通过某地铁公司开展的乘客满意度调查，可以看到，不同行车间隔下的乘客满意度数据曲线如图2 所示。

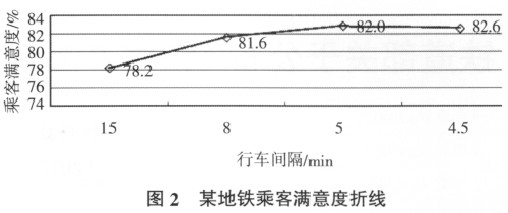
      由图 2 可以看出，当行车间隔压缩到一定程度时，候车时间的微弱变化对乘客已经不重要，压缩行车间隔的意义完全在于解决运能的问题。因此，如果根据不同区段客流差异实行大小交路套跑，不同区段可采用不同的行车间隔，这样可以在保证有效运能的情况下调整运用车数量，实现运营效益最大化。

      （2）压缩列车检修停时对于提高列车运能具有现实意义。

     目前，部分地铁公司通过均衡修、换件修等手段优化修程修制，甚至利用早晚高峰间隔安排维修作业，有效压缩了列车检修停时，减少了每日检修列车数，这样就促使有更多的列车投入正线运营服务，从而提高列车利用率，在列车配置数量不变的情况下增加运能。

      （3）必要时减少检修车数量对于提高列车运能应对爆发性增长的客流具有现实意义。

      在举办重大活动时，如北京奥运会、上海世博会、广州亚运会、深圳大运会等，客流出现爆发性增长，正常运用列车数量将无法满足营运需求，此时，可根据客流预测分析计算出最大用车需求，通过调整检修计划，减少检修车数量置换出更多的运用车进行弥补。

 

      针对地铁线路列车数量配置进行调查分析，充分考虑地铁高峰小时单向断面最大客流及列车最大核定载客量，建立了地铁线路列车配置数计算模型，应用计算模型对列车配置进行研究，通过实际统计数据分析、列车配置数反推验证了计算模型的有效性和实用性。实践中，模型中各个参数的灵活处理，能够使得在既有列车配置数下扩大和调整运能，这些经验已经在深圳地铁得到广泛运用，得到了相关运营、规划以及设计部门的一致认可，可以为其他地铁线路的规划、设计及运营提供参考。

 

［1］中华人民共和国交通运输部. 建标 104—2008 城市轨道交通工程项目建设标准［S］. 北京：人民交通出版社.