摘 要: 建立地铁车辆-轨道耦合动力学模型，将钢轨视为弹性离散点支撑的无限长 Timoshenko 梁，将实测钢轨短波波磨不平顺数据作为不平顺激励． 通过数值计算得到在科隆蛋扣件线路上不平顺发展过程中车辆动力学响应的变化情况． 随着短波波磨不平顺幅值的增大，轮对和转向架的横、垂向加速度以及轮轨横、垂向力均呈增大趋势，且受不平顺程度的影响较大． 结果表明钢轨波磨主要影响车辆系统的垂向振动．

关键词: 车辆-轨道耦合动力学; 钢轨波磨; 轮对; 转向架; 轮轨力

 

      为提高地铁系统的环境友好度，大量的减振降噪措施已经或即将被应用在地铁系统上: 如采用阻尼车轮和阻尼钢轨等降低轮轨滚动接触噪声; 轨道采用减振结构，减少车辆轨道振动对地铁沿线居民和建筑物的危害． 从减振级别、线路条件和经济成本等多方面考虑，通常在线路的不同区段采用不同的轨道减振措施． 常用的地铁轨道减振措施主要有套靴弹性短轨枕、减振扣件、梯形轨枕道床以及浮置板道床等． 目前，减振性能较好的扣件系统为科隆蛋( Cologne-egg) 扣件( 见图 1) ，但在某些地铁线路的实际使用过程中，科隆蛋扣件系统不仅没有达到预期的减振降噪目的，而且使得安装该扣件的直线和曲线线路上的钢轨在短时间内( 约 4 个月) 出现严重短波波浪形磨损． 钢轨短波波浪形磨损将大幅增加轮轨冲击载荷，导致过高的轮轨滚动接触噪声，缩短轮轨系统的使用寿命，降低地铁系统的环境友好度并增加运营成本．

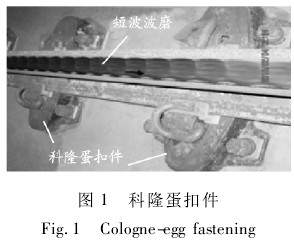
      钢轨波磨指其接触表面出现像波浪形的不均匀磨损．^［1］钢轨的不规则磨损和变形与轨道初始不规则的几何缺陷相叠加，导致列车通过时车辆轨道结构振动加剧，钢轨不均匀磨损和塑性累积变形加大．随着车辆通过次数的增多，钢轨顶面的不均匀磨损和塑性变形不断累积，逐渐形成波磨．^［2］按波长大小可将钢轨波磨分为长波波磨( 200 ～1 500 mm) 和短波波磨( 40 ～100 mm) ．^［3］钢轨波磨一直是铁路运输业难以解决的技术问题: 它的形成和发展导致车辆轨道产生强烈的振动和噪声，缩短车辆轨道结构零部件的使用寿命，影响列车的运行品质，严重的会导致列车脱轨．

      国内外学者就钢轨波磨进行大量的理论和试验研究: 文献［1］建立较完整的钢轨磨耗型波磨理论计算模型，并利用该模型计算各种可能的轨道缺陷对钢轨波磨形成和发展的影响; 文献［3］和［4］分析钢轨波磨对车辆轨道动态相互作用的影响，研究钢轨波磨发展过程对车辆轨道动态行为的影响，探索二者之间的内在联系，为判断钢轨是否需进行打磨提供参考． 本文建立地铁车辆-轨道耦合动力学模型，采用移动轨下支撑模型模拟离散的轨枕支撑对系统动力响应的影响． 通过数值计算，分析在科隆蛋扣件线路上短波波磨不平顺对地铁车辆动力学响应的影响． 评价指标主要包括轮对横、垂向加速度，转向架横、垂向加速度和轮轨横、垂向作用力等．

 

      为分析钢轨波磨发展对车辆动态响应的影响，建立地铁车辆-轨道耦合模型． 用多刚体动力学模型模拟车体、转向架和轮对等，车辆系统各部分结构用等效弹簧、阻尼连接． 车辆-轨道耦合动力学模型见图 2，图中符号的说明见文献［5］． 该模型考虑一、二系悬挂，整个车辆子系统共有 35 个自由度．

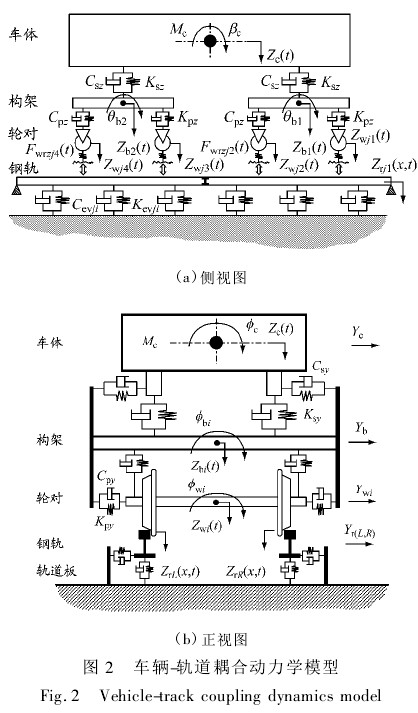
      在本文的轨道模型中，左、右钢轨被视为连续弹性离散点支撑基础上的 Timoshenko 梁，考虑钢轨垂向、横向和扭转方向的振动．由于本文重点研究钢轨短波波磨对车辆动力学性能的影响，而过去轨道模型中的欧拉梁钢轨模型考虑的频率范围比Timoshenko 梁模型频率范围低，对于本文短波波磨产生的高频激励，用 Timoshenko 梁模型能更真实地反映钢轨的特性． 钢轨形状系数是用 ANSYS 建立的真实钢轨截面有限元模型分析计算得到的．

      由于扣件刚度相对轨道板的支撑刚度小，轨道板的刚体运动相对较小，轨道板自身柔性变形运动频率较低，对轮轨和车辆高频响应的影响很小，所以不考虑扣件系统下部结构对系统高频响应的影响．轮轨法向力由赫兹非线性弹性理论确定，轮轨切向力由 Shen-Hedrick-Elkins 理论模型确定．^［6］

 

      科隆蛋扣件是在减振要求较高地段采用的轨道减振器扣件，自 1978 年以来，得到广泛应用和发展．该扣件支撑在轨板与底座之间，用减振橡胶硫化粘贴在一起，用橡胶圈剪切变形获得较低的竖向刚度，比 DTI 型扣件的振动传递减少 15 ～ 30 dB．^［7］依据科隆蛋扣件横、垂向加载-变形曲线( 见图 3) ，计算模型中使用的科隆蛋扣件的横、垂向刚度分别为7． 58 MN / m 和 12． 07 MN / m． 试验通过用力锤敲击轨头，利用加速度传感器测得钢轨横、垂向加速度衰减情况( 见图 4) ，运用半功率点法^［8］算得扣件的横、垂向阻尼分别为 974． 27 kN·s/mm 和1 361． 12 kN·s / mm．

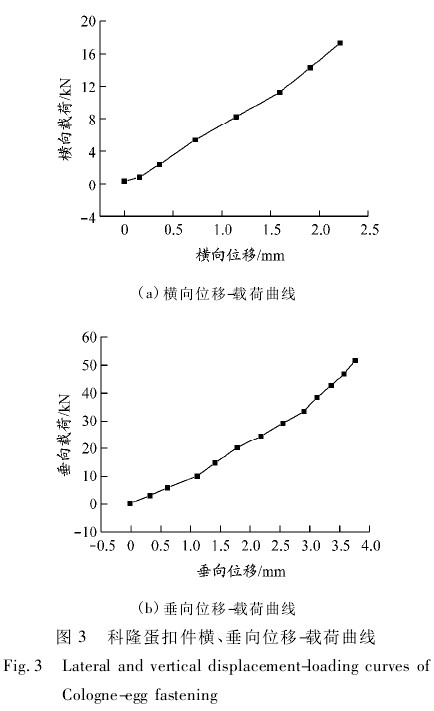
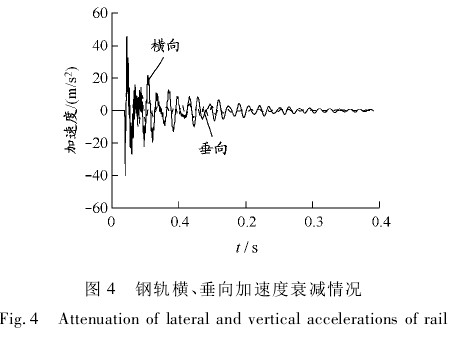
      在扣件阻尼参数敲击试验过程中，敲击的不是实际轨道，而是利用一个轨跨长度( 550 mm) 的实际钢轨作为质量块; 用扣件将其与刚性地面连接，这样扣件系统与该段钢轨构成单自由度阻尼系统; 再利用力锤分别敲击钢轨轨头的横向和垂向，得到图 4所示的脉冲响应; 用该响应曲线算得扣件的横、垂向阻尼系数．

 

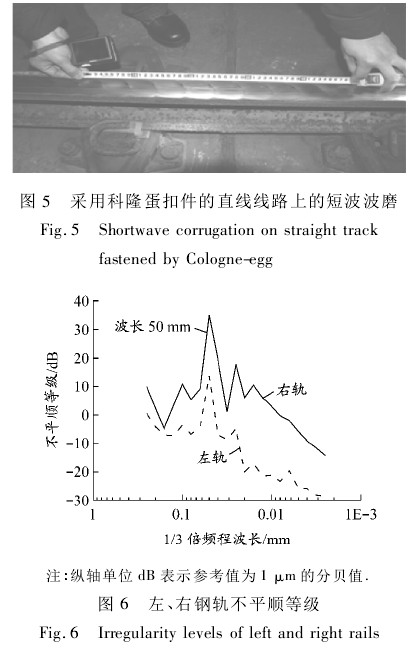
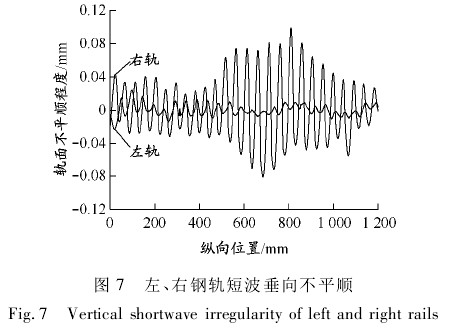
      现有的轨道谱包括美国五级、六级谱，德国谱和中国的三大干线轨道谱等，但至今还没有地铁线路的轨道谱． 从更符合中国铁路运输现状的角度看，本文轮轨激励的不平顺输入为实测的钢轨短波波磨不平顺数据． 直线钢轨出现波长约为 50 mm 的波磨，见图 5． 波峰与波谷之间有清晰的分界线，波峰、波谷的分布与钢轨顶面横向之间形成 15° ～ 20°的夹角． 波磨的特点是波长分布均匀、压痕清晰，波磨呈现材料以累积塑性流动为主，同时存在累积磨损． 现场测点位置左、右钢轨不平顺等级见图 6，左、右钢轨短波垂向不平顺见图 7． 可知，左轨最大不平顺等级为17 dB，最大波峰与波谷差约为0． 038 mm; 右轨最大不平顺等级为 35 dB，最大波峰与波谷差约为0． 206 mm． 在该侧点位置，右轨波磨比左轨严重．

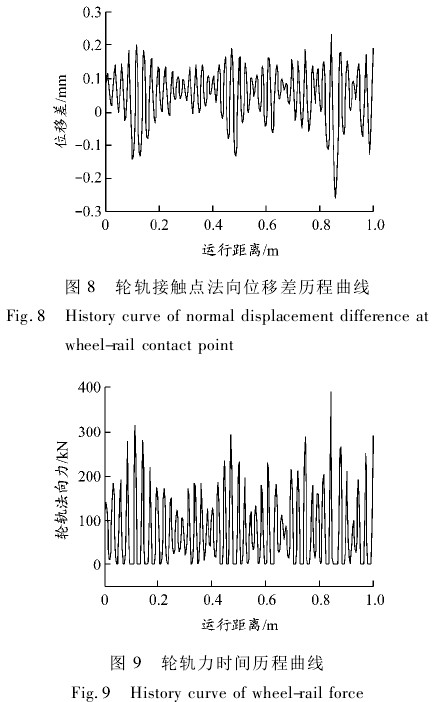
      在计算轮轨力时，首先根据轮轨踏面位置状态搜索轮轨接触点，然后计算接触点的法向位移差，再根据法向位移差采用 Hertz 接触理论计算轮轨力．当法向位移差为负值时，出现轮轨分离现象，此时轮轨力为 0． 当车辆以 60 km/h 速度运行时，在实测钢轨短波波磨激励( 见图 7) 下，第一轮对右轮的轮轨接触点法向位移差历程曲线见图 8．当位移差为负值时表示轮轨分离，出现轮轨力为 0 的现象( 见图9) ; 当轮轨从分离状态转变为接触状态时，会出现轮轨冲击现象，产生很高的轮轨冲击力( ＞300 kN) ．

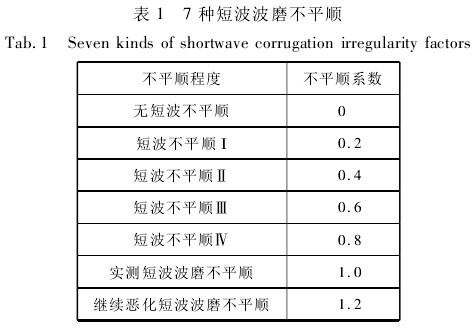
      为近似模拟波磨发展过程中车辆动力学响应的变化情况，将测得的钢轨垂向不平顺幅值数据分别乘以系数，得到 7 种短波波磨不平顺( 见表 1) ，并将其作为不平顺激励输入．

      轮对横、垂向最大加速度随不平顺程度变化曲线见图 10，可知，轮对横、垂向最大加速度均随不平顺程度的增大而增大，且波磨程度对轮对横、垂向加速度的影响非常大．

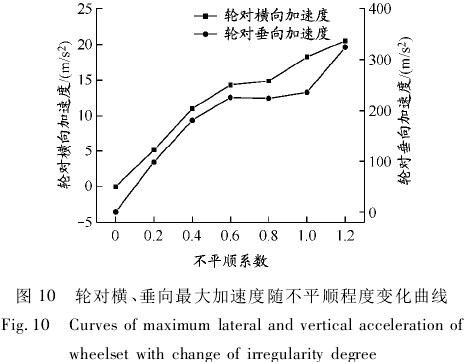
      转向架横、垂向最大加速度随不平顺程度变化曲线见图 11，可知，转向架横、垂向最大加速度随不平顺程度的变化情况和轮对加速度一致． 由于一系悬挂系统的减振作用，使得转向架的垂向加速度远小于轮对的垂向加速度，而横向加速度的减小量却没有垂向那么明显，说明钢轨波浪形磨损主要影响车辆系统的垂向振动． 第一轮对左、右车轮最大轮轨垂向力随不平顺程度变化曲线见图 12． 对照图 6 中轨面不平顺等级可知，由于右钢轨短波波磨不平顺等级高于左钢轨，右轮所受垂向力均大于左轮所受垂向力，且随着短波波磨不平顺激励程度的加剧，右轮受到的轮轨横垂向力的增幅明显大于左轮受到的增幅． 其他轮对左、右轮轨力的变化趋势与第一轮对的变化趋势一致，故不再列出． 另外，由图 12 可知，在受实测短波波磨不平顺激励时，轮轨垂向力已超过 350 kN，这种轮轨间冲击会进一步破坏轮轨接触面，使原有钢轨轨面受波磨程度恶化，进而产生更大的轮轨噪声．

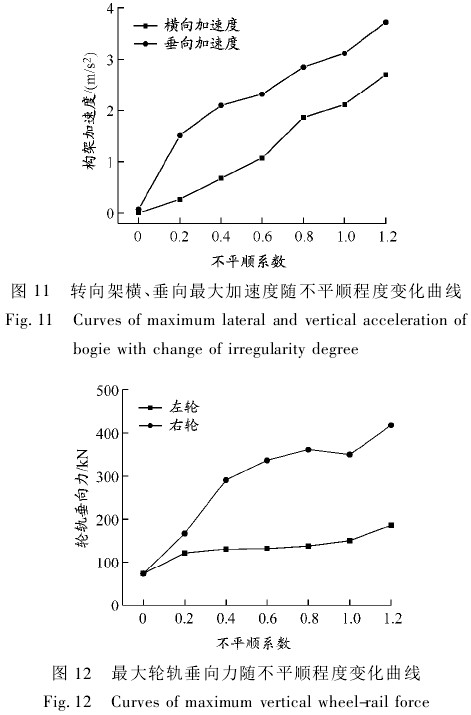
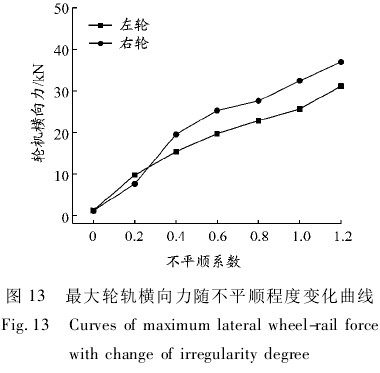
      最大轮轨横向力随不平顺程度变化曲线见图13，可知，随着短波波磨不平顺程度的增大，左、右轮轨横向力均呈增大趋势，且右轮最大横向力比左轮大，这与轮轨垂向力的变化趋势一致． 其他轮对最大横向力的变化趋势与第一轮对的变化趋势一致．

 

      建立地铁车辆-轨道耦合动力学模型，采用数值分析方法模拟地铁车辆在科隆蛋扣件的板式轨道线路上运行时，不同程度钢轨波磨不平顺对车辆轨道动力学响应的影响． 由计算结果可知: ( 1) 轮对和转向架的横、垂向振动加速度随不平顺程度的增大而增大; ( 2) 钢轨波浪形磨损主要影响车辆系统的垂向振动; ( 3) 轮轨横、垂向力随不平顺程度的增大而增大，当钢轨存在波浪形磨损时会使轮轨间产生非常大的冲击．

 

［1］ 温泽峰． 钢轨波浪形磨损研究［D］． 成都: 西南交通大学，2006．

［2］ 金学松，温泽峰，王开云． 钢轨磨耗型波磨计算模型与数值方法［J］． 交通运输工程学报，2005，5( 2) : 13-18．

          JIN Xuesong，WEN Zefeng，WANG Kaiyun． Theoretical model and numerical method of rail corrugation［J］． J Traffic ＆ Transportation Eng，2005，5( 2) : 13-18．

［3］ CLARK R A，FOSTER P． On the mechanics of rail corrugation formation［J］． Vehicle System Dynamics，1983，12( 1) : 35-39．

［4］ 周永健，练松良，杨文忠． 轨面短波不平顺对轮轨力影响的研究［J］． 华东交通大学学报，2009，24( 6) : 6-12．

          ZHOU Yongjian，LIAN Songliang，YANG Wenzhong． Research of impact of short wave track irregularity on the wheel-rail force［J］． J East China Jiaotong Univ，2009，26( 4) : 6-12．

［5］ 翟婉明． 车辆-轨道耦合系统动力学［M］． 3 版． 北京: 科学出版社，2007: 48-53．

［6］ 金学松，刘启跃． 轮轨摩擦学［M］． 北京: 中国铁道出版社，2004: 47-63．

［7］ 袁俊． 地铁浮置板轨道结构减振研究［D］． 西安: 西安建筑科技大学，2008．

［8］ 李宏年，陈丹华． 弹条Ⅰ型轨道扣件动力参数的试验研究［J］． 北方交通大学学报，1999，23( 4) : 87-90．

          LI Hongnian，CHEN Danhua． Research on the experiment of dynamic parameters of the railway fastener spring rod［J］． J Northern Jiaotong Univ，1999，23( 4) : 87-90．